PullingOutHair
- 2
- 0
Homework Statement
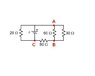
Four resistors are connected in a circuit with a battery of unknown emf, as shown below. The battery is ideal, so it has no internal resistance. The current in the 30Ω resistor is 100. milliamps.
C) Calculate power dissipated by the 20Ω resistor in watts.
D)Calculate the current in the battery in milliamps
Homework Equations
P=V2/R
V=RI
The Attempt at a Solution
Parts A and B of this question involved finding the current in the 60Ω resistor, and then the current in the 80Ω resistor, which I was able to do, getting 50mA and 150mA respectively. I'm not sure what that has to do with C and D. The problem with finding power is I do not know voltage. I thought I could get that easily, knowing I=150mA for the 80Ω resistor (V=IR=4.8V), but this doesn't work out, so I'm guessing I did something wrong there.
I'm really at a loss, so if somebody could help me step by step through this, it would be a big help.