physninj
- 37
- 0
Homework Statement
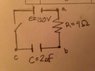
A simple RC circuit with an EMF source ε, Resistor R and capacitor C are in series. When the switch is closed find the rate of energy stored in the capacitor, the power dissipated in the resistor, and the power supplied by the emf as functions of time.
Homework Equations
For the resistor
P=i2R
i=(ε/R)e-t/RCFor the battery
P=iε
i=(ε/R)e-t/RC
For the capacitor
q=CE(1-e-t/RC)
U=q2/(2C)
The Attempt at a Solution
I feel decent about the expressions I got for the resistor and the battery.
Pres=[(ε/R)e-t/RC]2R
Pbat=[(ε/R)e-t/RC]εThe problem I'm having is getting the energy rate in the capacitor. I tried to just use the energy equation from above and divide by time but I don't think it's right, It's undefined at t=0, and I need to evaluate these equations at that point in later steps.
I think I may need to plug it into the energy and then take the time derivative. Its pretty messy though, is there a better way?
[CE(1-e-t/RC)]2/(2Ct)
Thanks for any input
Attachments
Last edited: