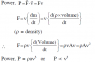- #1
Vibhor
- 971
- 40
Homework Statement
Homework Equations
The Attempt at a Solution
Power is given by F.v , but I am not sure how to calculate F in this case .Again 'v' is the speed of the point of application of force F . I also do not understand how force applied on blades is causing work .
Any help is appreciated .
Thanks