But the relative angle is not known until the last minute. The situation is the following:
View attachment 217546
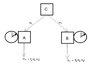
You have three devices: C, which is a source of message pairs, simulating photon pair production, and A and B, which simulate the measurement events.
- Every "round", C sends out a pair of messages, m_A to A and m_B to B.
- After the messages are sent, but before they are read, settings for A and B are chosen, independently. The settings are two angles, \theta_A and \theta_B.
- Device A determines an output, R_A(\theta_A), which is either +1 or -1, based on the message received from C and the setting \theta_A.
- Similarly, device B determines an output, R_B(\theta_B) based on its message and setting.
- Over many, many rounds, we can gather statistics for the correlation: \langle R_A(\theta_A) R_B(\theta_B) \rangle as a function of the pair of settings, \theta_A, \theta_B.
Bell's inequality implies that |\langle R_A(\theta_A) R_B(\theta_B) \rangle| \leq 2, no matter what algorithms are used by A, B, and C, as long as
- There are no communications among A, B, C other than those specified.
- The settings \theta_A and \theta_B for each round are unpredictable by C.
On the other hand, if instead of C sending messages, it generates a pair of entangled photons, and sends one to A and one to B, then you can violate the inequality. (Inside A and B, instead of a computer algorithm, you have polarizing filters and photon detectors, and each sends out +1 if the photon passes through the filter at the orientation specified by \theta_A or \theta_B.