Pressure gradient in wakes around a cylinder

[dRic2]

Hi,

Let's consider a cylinder of infinite length and fluid flowing "over" (I'm not sure of which words I should use, sorry) it like in the figure:

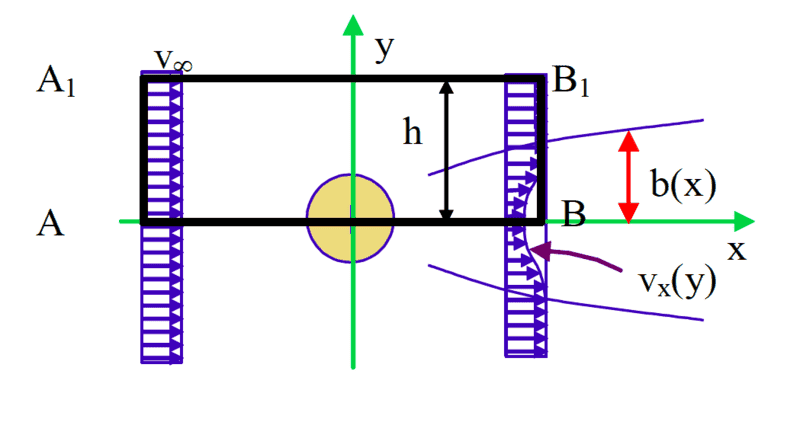
Let's consider x>>D in order to neglect what's happening near the rear surface of the cylinder.

Let's get rid of static pressure which doesn't play a role here:

$$\nabla P = \nabla P_{s} + \nabla P_{d}$$

(where $P_s$ refers to static pressure while $P_d$ refers to dynamic pressure)

$$ \frac {D \mathbf v} {Dt} = \nabla \tau - \nabla P_{s} - \nabla P_{d} + \rho \mathbf g $$

Being $\nabla P_s = -\rho \mathbf g$:

$$ \frac {D \mathbf v} {Dt} = \nabla \tau - \nabla P_{d} $$

Okay, now I found on a book that since x>>D the influence of the object on the flow is minimum so the small changes in the velocity profile suggest that $\nabla P_{d} = 0$, obtaining the simplified equation:

$$ \frac {D \mathbf v} {Dt} = \nabla \tau $$

Well, it is not clear to me this last step. If $\nabla P = 0$ how is the fluid supposed to move?? Wouldn't $\frac {D \mathbf v} {Dt}$ and $\nabla \tau$ be $0$ as well ($0=0$)?

 

[boneh3ad]

I am a little confused about what you are doing here. It appears that you tried to write down the Navier-Stokes equations but it isn't correct. First, there should be a $\rho$ term over by your velocity derivative. That could just be a typo, however, but the rest of it has more fundamental problems. In particular, the pressure term in the Navier-Stokes equations has nothing to do with dynamic pressure. It refers only to the thermodynamic (or static) pressure. Further, you somehow equated the static pressure gradient with the negative of the gravitational body force, which doesn't seem to make sense in the context of this problem.

I have a feeling you have a fundamental misunderstanding of what static and dynamic pressure actually are. The momentum equation should be
\rho\dfrac{D\vec{v}}{Dt} = \nabla \cdot \tau + \rho \vec{g} = -\nabla p + \nabla \cdot \tau_v + \rho \vec{g}.
Here I made the distinction between $\tau$, the stress tensor, and $\tau_v$, the viscous stress tensor. The important thing here is that, again, the $p$ referenced here is thermodynamic (static) pressure. Any talk of the dynamic pressure is wrapped up in that $\vec{v}$ term on the left-hand side (and its components inside of $\tau_v$ of course).

With all that in mind, I don't think your question makes sense.

Also note that a fluid can flow while $\nabla p=0$. It just can't accelerate (and will likely decelerate if the flow is viscous).

 

[dRic2]

Well thank you very much. You just confirmed the fact that I'm totally lost. The problem is that this is exactly what is written in my professor's book (it's in italian though).

First of all the pressure. I know this is illogical but my prof. does this very often. Here I post a scan of his "book" so you can see (although it's in italian you can still understand the formulas):

See? If you want to know what he says in between I can translate but I think it is useless

 

[boneh3ad]

It's possible he is defining static and dynamic pressure in an unconventional way. Usually static pressure, $p$, is taken to mean the thermodynamic pressure and the dynamic pressure is taken to mean
q = \dfrac{1}{2}\rho |\vec{v}|^2.
Total pressure is then usually
p_t = p + q.
I can make out some of the text based on my familiarity with Spanish, but a fair bit eludes me as well. It doesn't look like it contains the information required to figure out what he means, though.

 

[dRic2]

It doesn't look like it contains the information required to figure out what he means, though.

It doesn't for sure ahaha

BTW, as you said, in NS equation $P$ refers to static pressure so I still don't understand

 

[dRic2]

@boneh3ad I don't want to bother you, but I'm a bit confused right now. Since you said $\nabla P$ refers only to static pressure in NS equations,

is this wrong?

 

[boneh3ad]

Without knowing the full context of that equation I don't think I could say for sure. It does seem wrong, though.

 

[dRic2]

Without knowing the full context

There isn't very much to say... It's just NS equations and he wants to apply them to this case. From what I understood the aim is to say $\nabla P$ and $\rho \mathbf g$ are negligible and write (for bi dimensional and stationary flow):

$$v_x \frac {\partial v_x} {\partial x} + v_y \frac {\partial v_x} {\partial y} = \frac {\partial \tau_{xx}} {\partial x} + \frac {\partial \tau_{xy}} {\partial y}$$
$$v_x \frac {\partial v_y} {\partial x} + v_y \frac {\partial v_y} {\partial y} = \frac {\partial \tau_{yx}} {\partial x} + \frac {\partial \tau_{yy}} {\partial y}$$

My problem is that I don't know how to reach this equation since I don't understand what he's doing to get it

 

[boneh3ad]

Right but he may have a nonstandard definition of his stress tensor. How does he define $\underline{\underline{\tau}}$?

Sorry for the weird double underline. Apparently that's just how this site's LaTeX interpreter operates.

 

[dRic2]

Apparently he defines the stress tensor (for Newtonian fluids) as $\tau = -\mu \left ( \frac {\partial v_i} {\partial x_j} + \frac {\partial v_j} {\partial x_i} \right )$ (I'm not sure about the sign though) which is the standard way I think

I don't know how to write tensors either...EDIT: I think $\tau = \mu \left ( \frac {\partial v_i} {\partial x_j} + \frac {\partial v_j} {\partial x_i} \right )$ is the correct one, since then he writes NS equations as $\rho \frac {D \mathbf v} {Dt} = \mu \nabla^2 \mathbf v - \nabla P + \rho \mathbf g$

 

[boneh3ad]

He would need the negative sign since he has a negative in the original equation to make the sign work out. Anyway, if he insists on using "total" pressure in that pressure term, that could be split up into static and dynamic, that would look like
\nabla p_t = \nabla p + \dfrac{V^2}{2}\nabla\rho + \rho\vec{v}\cdot\nabla\vec{v}
So, assuming $\nabla\rho = 0$, the form he uses almost makes sense, but only if the LHS had a simple partial derivative with respect to time and not a material derivative. That is, assuming he is using standard definitions of total, static, and dynamic pressure.

I don't think I've missed anything here, but I can't rule it out. At the very least, his method of working with this seems to be rather unusual.

 

[dRic2]

I thought of that, but if we accept the mistake and use $\frac {\partial v} {\partial t}$ then there is an other problem. Since he neglects pressure (later on) he would also have to neglect $\rho v ⋅ \nabla v$, but then he can't write

$$v_x \frac {\partial v_x} {\partial x} + v_y \frac {\partial v_x} {\partial y} = \frac {\partial \tau_{xx}} {\partial x} + \frac {\partial \tau_{xy}} {\partial y}$$
$$v_x \frac {\partial v_y} {\partial x} + v_y \frac {\partial v_y} {\partial y} = \frac {\partial \tau_{yx}} {\partial x} + \frac {\partial \tau_{yy}} {\partial y}$$

because it would be

$$ 0 = \frac {\partial \tau_{xx}} {\partial x} + \frac {\partial \tau_{xy}} {\partial y}$$
$$ 0 = \frac {\partial \tau_{yx}} {\partial x} + \frac {\partial \tau_{yy}} {\partial y}$$

I'm lost and I don't want to abuse your patience ,but is there an other method to reach the above equation?

 

[boneh3ad]

Not that I see clearly.

 

[dRic2]

I'll try to contact him, I don't see an other way...