Pressure in an inverted cylinder partially filled with water

AI Thread Summary
The discussion centers on the pressure dynamics in an inverted cylinder partially filled with water. It clarifies that the pressure of the air inside the cylinder (P_air) acts upwards, contrary to the initial assumption that it acts downwards. The equation provided, P_cylinder = -(P_air + P_water), indicates that both P_air and P_water contribute to the upward force against the downward forces, which include the weight of the plate and the water. The key takeaway is that the total pressure acting on the plate is a balance of these forces. This understanding resolves the confusion about the direction of P_air's influence.
zerogoal
Messages
21
Reaction score
0
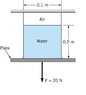
Hi may i know if the pressure of air in the cylinder is acting upwards or downwards? I know the pressure of the cylinder is acting downwards and the pressure of water is acting upwards.

My teacher gave me this equation Pcyclinder= -(Pair + Pwater)

However i do not know why Pair is acting in the same direction as Pwater. I thought Pair should be acting downwards, acting on the water instead?

Can someone help me with this? Thanks
 

Attachments

  • cylinder.jpg
    cylinder.jpg
    5.3 KB · Views: 1,372
Physics news on Phys.org
P_air is the pressure of the air INSIDE the cylinder. you basically have 2 forces acting on the plate, up and down. The "up" force is atmospheric pressure that you can calculate knowing the pressure and the surface area. The "down" force is actually the sum of 3 forces. The weight of the plate, the weight of the water (pressure of the water), and the pressure, P_air, of the air inside the cylinder.
 
hey thanks for taking the time to help me with this question. finally understood.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Volume's effect on buoyancy: Does pressure increase?
Replies
11
Views
2K
Why is it necessary to start this experiment with the water level at 400mL?
Replies
35
Views
2K
What is the relationship between pressure and flow rate?
Replies
8
Views
4K
Why Does Surface Tension Allow Bubbles to Form Despite External Pressure?
Replies
3
Views
883
Buoyant Force Question: Cylinder and Cone in Water - Homework Solution
Replies
5
Views
2K
Atwood's with a cylinder - Rotational Motion
Replies
13
Views
858
Sinking a cylinder with varying hole sizes
2
Replies
97
Views
13K
Solving an Air Pressure Question: Who Is Right?
Replies
5
Views
2K
A water-bottle demonstration of atmospheric pressure
Replies
6
Views
2K
Calculate the resulatant downward force of a submarine on the seafloor
Replies
11
Views
3K

Hot Threads

Recent Insights

Back
Top