Guilty Spark
- 31
- 0
Pressurized air in aluminum block.. help so it doesn't explode!
Hey everybody! Need some help with a design I'm comming up with for myself- it's an air valve block.
What I'm having trouble with is figuring out how close I can make the holes to each other?
I don't have any computing software that does this sort of thing or calcuations so I whiped up something in MS paint to show you:
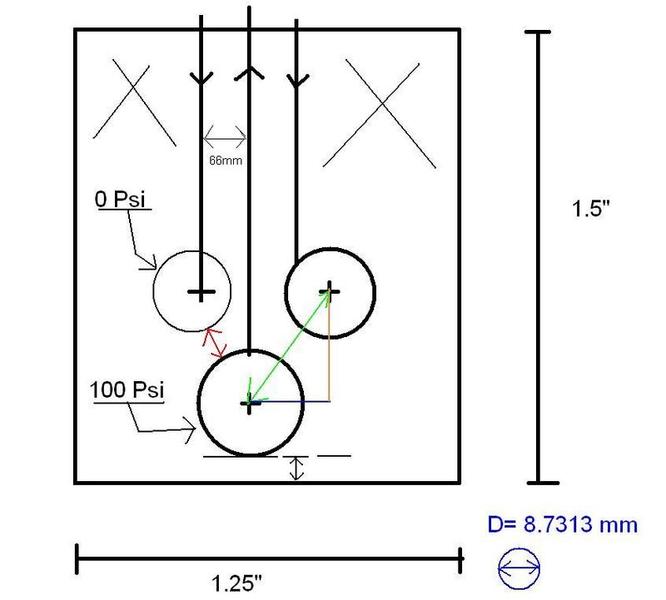
The diameter in mm is there, max psi will be 100 (maybe 110 to be safe..).
The center hole is in the exact center of the block with one passage. The other two passages are 66mm on each side.
The passages for the air are fixed, but the holes can be moved off center (I think?) as they are just exhausting to atmosphere. Shouldn't affect it right?
Material is 6061-T6 Aluminum.. I would find a value for you in regards to pressure rating but I don't know which one I am looking for?
----
Summary:
All holes same diameter. Able to offcenter the two from their passages.
Looking to keep holes as far down as possible to allow for more stuff in the top of the block.
-How far off bottom should the hole be?
-How close can the other two holes be to the pressurized one, and it's pressurized air passage.
(Give green line value if you can, as I want to trace a line with a compass off the center mark of the bottom one)
-Assuming 110psi including safety margin.
---
Thx, and any questions feel free to post!
Hey everybody! Need some help with a design I'm comming up with for myself- it's an air valve block.
What I'm having trouble with is figuring out how close I can make the holes to each other?
I don't have any computing software that does this sort of thing or calcuations so I whiped up something in MS paint to show you:
The diameter in mm is there, max psi will be 100 (maybe 110 to be safe..).
The center hole is in the exact center of the block with one passage. The other two passages are 66mm on each side.
The passages for the air are fixed, but the holes can be moved off center (I think?) as they are just exhausting to atmosphere. Shouldn't affect it right?
Material is 6061-T6 Aluminum.. I would find a value for you in regards to pressure rating but I don't know which one I am looking for?
----
Summary:
All holes same diameter. Able to offcenter the two from their passages.
Looking to keep holes as far down as possible to allow for more stuff in the top of the block.
-How far off bottom should the hole be?
-How close can the other two holes be to the pressurized one, and it's pressurized air passage.
(Give green line value if you can, as I want to trace a line with a compass off the center mark of the bottom one)
-Assuming 110psi including safety margin.
---
Thx, and any questions feel free to post!