desmond iking
- 284
- 2
Homework Statement
i am having problem on part e , the ans given is 504-(7c1 X4 )= 476
but my working would be 504-(7c1 X4 x2 )= 448
since the pure maths and statistics can be arranged in 2! ways , but the 1 tem which is chosen from 7 items can be placed in 4 location , just as in the picture.
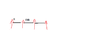
![IMG_20140724_014823[1].jpg](/data/attachments/55/55028-8280cbce5456705bcca40756ddde8c2c.jpg?hash=goDLzlRWcF)