- #1
pp123123
- 6
- 0
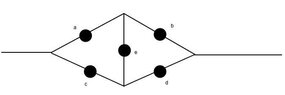
Hi guys. Here's the problem.View attachment 1981
I need to determine the probability that the current could go from left to right given that there is a probability of p for each independent switch named a,b,c,d and e.
I have tried to solve this but I have no idea which part I am getting off the right track. Here is what I am trying to do.
Case I: Assume Switch E is closed so I have a probability of
P((AB) or (CD))=P(AB)+P(CD)-P(AB and CD)=2p^2-p^4
Case II: Assume Switch E is opened so I have a probability of
P((A or C) and (B or D))=(P(A)+P(C)-P(AC))(P(B)+P(D)-P(BD))=(2p-p^2)^2
so overall probability is (1-p)(2p^2-p^4)+p(2p-p^2)^2 which could be simplified to 2p^5-5p^4+2p^3+2p^2
however some friends of mine told be that it should be p^5-5p^4+2p^3+2p^2. I hope to know what's wrong in my calculation. Thanksss!
I need to determine the probability that the current could go from left to right given that there is a probability of p for each independent switch named a,b,c,d and e.
I have tried to solve this but I have no idea which part I am getting off the right track. Here is what I am trying to do.
Case I: Assume Switch E is closed so I have a probability of
P((AB) or (CD))=P(AB)+P(CD)-P(AB and CD)=2p^2-p^4
Case II: Assume Switch E is opened so I have a probability of
P((A or C) and (B or D))=(P(A)+P(C)-P(AC))(P(B)+P(D)-P(BD))=(2p-p^2)^2
so overall probability is (1-p)(2p^2-p^4)+p(2p-p^2)^2 which could be simplified to 2p^5-5p^4+2p^3+2p^2
however some friends of mine told be that it should be p^5-5p^4+2p^3+2p^2. I hope to know what's wrong in my calculation. Thanksss!