(Probably) simple question: Asymptotes of a Hyperbola

[sltungle]

Okay, before I start: I'm sorry for what is probably going to be an absurdly easy question and I'm probably going to seem like a complete moron to everyone here, however the way I see it the only way I'll learn is by asking questions (and that's just what I've did ever since I could speak)... so... help would be appreciated.

Find the asymptotes for the hyperbola: 2x^2/3 - y^2/2 = 1



Equations: Hyperbola: (x-h)^2/a^2 - (y-k)^2/b^2 = 1, Asymptote: ±b/a (x-h) + k



Attempt:

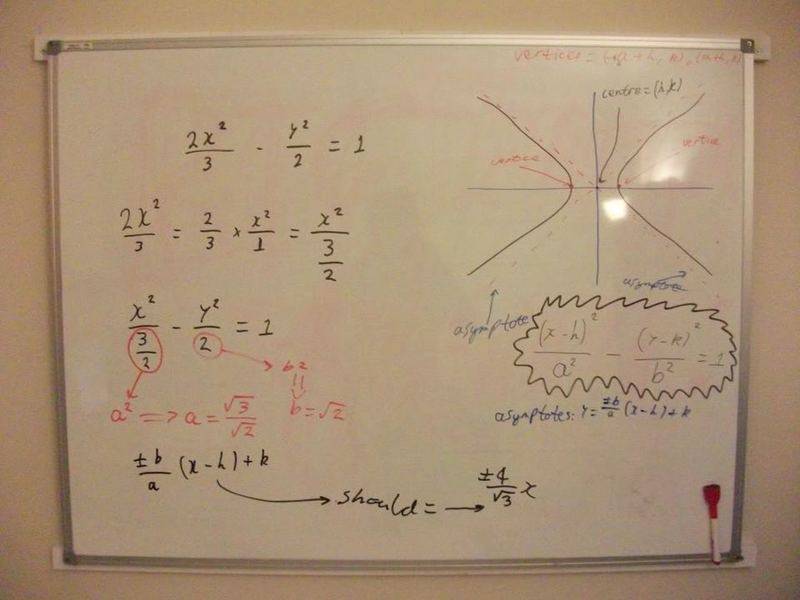
I keep arriving at the answer ±2/√3 yet the answer in the back of the book is ±4/√3. What am I doing wrong?

 

[HallsofIvy]

Here's the easy way to think about "asymptotes". The whole point of asymptotes is that the hyperbola gets closer and closer to them as x and y get larger and larger. Now if x is extremely large, x^2 will be even larger and so will x^2/a^2 for constant a. Similarly, y^2/b^2 will be an extemely large number. Comparatively, the "1" on the right side of the equation is very small and negligible. If we drop it from the equation of the hyperbola, we get
\frac{x^2}{a^}- \frac{y^2}{b^2}= 0
\left(\frac{x}{a}- \frac{y}{b}\right)\left(\frac{x}{a}+ \frac{y}{b}\right)= 0

From that, x/a= y/b and x/a= -y/b are the two asymptotes.

Here, 2x^2/3= x^2/(3/2) so a= \sqrt{3/2} and b= \sqrt{2}.

The asymptotes are given by x/(\sqrt{3/2}= y/\sqrt{2} so that y= \sqrt{2}x/\sqrt{3/2}x= (2/\sqrt{3})x and x/\sqrt{3/2}= -y/\sqrt{2} so that y= -(2/\sqrt{3})x.

You are right and the book is wrong!

 

[sltungle]

Ahh. Thank you very much :) I was a bit worried I was missing something obvious. Glad to know I'm not.

Thanks again.

 

[JsStewartFan]

Dear HallsofIvy,

Thanks for your easy-to-follow explanation of why you replace the 1 with a zero to find the asymptotes. I had gotten that tidbit from another website, but they didn't explain why you set the original equation to 0 instead of 1.

 

[gb7nash]

As a side note, I want your whiteboard.