walker
- 28
- 0
alright the question asks
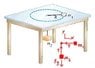
An air puck of mass m1 is tied to a string and allowed to revolve in a circle of radius R on a frictionless horizontal table. The other end of the string passes through a hole in the center of the table, and a counterweight of mass m2 is tied to it (see the figure below). The suspended object remains in equilibrium while the puck on the tabletop revolves.
(Use g for free fall acceleration)
Find the tension T on the string.
Find the radial force Fc acting on the puck
Find speed v of the puck
What I've come up with is
T = m2g - m1(v^2/R)
Fc = m1(v^2/R)
v = sqrt[(Fc*R)/m1]
For some reason I'm finding the question to be too ambigious and i am second guessing what i am doing. Also I have nothing to really go by in the way of lecture notes or example textbook problems that can aid me with this question. if someone could shed some light that would be awesome.
ive included a diagram and drawn on it what i think the forces are.
An air puck of mass m1 is tied to a string and allowed to revolve in a circle of radius R on a frictionless horizontal table. The other end of the string passes through a hole in the center of the table, and a counterweight of mass m2 is tied to it (see the figure below). The suspended object remains in equilibrium while the puck on the tabletop revolves.
(Use g for free fall acceleration)
Find the tension T on the string.
Find the radial force Fc acting on the puck
Find speed v of the puck
What I've come up with is
T = m2g - m1(v^2/R)
Fc = m1(v^2/R)
v = sqrt[(Fc*R)/m1]
For some reason I'm finding the question to be too ambigious and i am second guessing what i am doing. Also I have nothing to really go by in the way of lecture notes or example textbook problems that can aid me with this question. if someone could shed some light that would be awesome.
ive included a diagram and drawn on it what i think the forces are.
Attachments
Last edited: