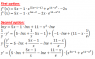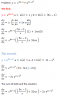So, I gave the x
5x-1 term to WolframAlpha to differentiate.
WolframAlpha did not use logarithmic differentiation. Instead, it used the following scheme.
Suppose we have a function that can be expressed in the following way,
\displaystyle f(x)=g\left(u(x),\,v(x)\right)
then the derivative of f(x) can be obtained as follows.
\displaystyle \frac{d}{dx}f(x)=\frac{d}{dx}g\left(u(x),\,v(x) \right)=\frac{\partial g(u,v)}{\partial u}\frac{d\,u(x)}{dx}+\frac{\partial g(u,v)}{\partial v}\frac{d\,v(x)}{dx}
For the case of \displaystyle f(x)=x^{5x-1}\,, we have \displaystyle g(u,\,v)=u^v\,, where \displaystyle u(x)=x\,, and \displaystyle u(x)=5x-1\,.
∂g/∂u treats the function g, as if the base of the expression, in this case x by itself, is the part with the variable, and treats the exponent as being constant, as is the case of a power function.
∂g/∂v treats the exponent of the expression, in this case x by itself, as being the part with the variable, and treats the base as being constant, as is the case of an exponential function.