Problem on tangents to a cirlce

[anantchowdhary]

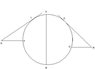
Suppose we have a cirlce with diameter AB.P and Q are points on opposite sides of te diameter(both points are on the circumference).Now PR=QM where R and M are also on opposite sides and on the same sides of P and Q outside the circle.

Now if we draw tangents from R and M,how do we prove that they will be equal in length?

We basically have to prove RL=MG taking RP =QM

if L and G are the contact points

 

[mathman]

Your assumption is that RP=QM. Let C be the center. First RC=MC, since you are adding radii to the known pieces sticking out. Next, LC=GC (both radii). Therefore you have two right triangles with hypotenuses equal, and also equality in one leg. Therefore the other leg pair (RL and MG) are also equal.

This looks like an elementary geometry exercise.

 

[anantchowdhary]

But P and Q and C arent necessarily collinear

 

[uart]

anantchowdhary, you haven't fully specified the problem. What is the direction of PR and QM? Are they both radial, or are they both perpendicular to AB or are they something else.

 

[anantchowdhary]

they arent radial and they arent parallel to each other.we just know that
RP=QM

 

[uart]

they arent radial and they arent parallel to each other.we just know that
RP=QM

Then RL and MG certainly need not be equal

 

[anantchowdhary]

RL and MG will be equal only
when if the lines RP and QM produced intersect the same diamter necessarily

 

[uart]

RL and MG will be equal only
when if the lines RP and QM produced intersect the same diamter necessarily

What, each one intersects the diameter, that's all. Or do you mean that they intersect each other at the diameter. You need to specify the problem correctly and fully.

 

[anantchowdhary]

NO,they do not intersect each other.If produced backwards(RP and QM),they would have to intersect the same diamter.And also,any one of them when produced can't be the diameter,or both of then have to be diameters.Is it ok now?