MHB Problem solving 2 variable equal triangle problem

[jeflon]

I solved this many years ago, but after revisiting Trig in order to tutor my daughter, I revisited this to stimulate myself but am hitting a brick wall.

Problem:
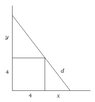
A 4 inch square sits in a corner(picture x,y origin). A 12 inch ruler or line leans against the wall at an angle such that there are 3 points of contact: wall, the outer corner of the block, and the floor.
At what point on the ruler does the corner of the block make contact?

Efforts:
We know that the upper triangle and lower triangle are of same angles. (Ruler passes through 2 parallel lines, being the floor and the top of the 4 inch block. So the trig function ratios are equal.
I have gone the route of setting the large triangle hypotenuse (12) equal to the sum of the hypotenuses of the smaller triangles leading me down a path that still leaves me with 2 variables.

I would appreciate some input as to a fresh way of approaching this problem, not necessarily the answer.

 

[MarkFL]

I would draw a diagram:

View attachment 2006

By similarity, we have:

$$\frac{y}{4}=\frac{4}{x}\implies y=\frac{16}{x}$$

Using the Pythagorean theorem on the large triangle, we may write:

$$(x+4)^2+(y+4)^2=12^2$$

Now using the expression for $y$ in terms of $x$ to get an equation in one variable. Once you have $x$, then you may determine $d$ using the Pythagorean theorem where:

$$x^2+4^2=d^2$$

 

[jeflon]

Many thanks, I had your step one and two but it was after making it more complicated than it needed to be and going off in wrong directions.
thanks again.

 

[Prove It]

I would draw a diagram:

https://www.physicsforums.com/attachments/2006

By similarity, we have:

$$\frac{y}{4}=\frac{4}{x}\implies y=\frac{16}{x}$$

Using the Pythagorean theorem on the large triangle, we may write:

$$(x+4)^2+(y+4)^2=12^2$$

Now using the expression for $y$ in terms of $x$ to get an equation in one variable. Once you have $x$, then you may determine $d$ using the Pythagorean theorem where:

$$x^2+4^2=d^2$$

I would be inclined to write that the entire horizontal length from the origin to the ruler as being length x, considering it's the position it will take on the x axis...

 

[jeflon]

I would be inclined to write that the entire horizontal length from the origin to the ruler as being length x, considering it's the position it will take on the x axis...

I went that direction also in some of my attempts, labeling unknown x,y with respect to large triangle as x-4 and y-4 respectively.