Problem with calculating magnetic flux for a single coil of wire.

[Zatman]

Homework Statement

This is more of a general question about magnetic flux in a uniform magnetic field, but I think this is the correct place to post it.

I understand that magnetic flux through an area A is the product of the magnetic flux density B and the projection of area A onto a surface perpendicular to the field.

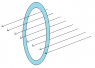
What I don't understand is the way it works for a coil of wire, say just one loop lying perpendicular to the field. I don't understand why you take the area as being the area of the physical circle created by the loop - i.e. pi*r² where r is the radius of the circle created by the loop. Surely it should be just the area of the wire?

Homework Equations

φ = BAcosθ
(which becomes φ = BA for this example)

The Attempt at a Solution

If you take a straight wire, the area you take would be the length of the wire times the diameter. So why is it that when you coil that wire around the flux changes because you apparently take the area of the circle it describes? How does the empty space in the middle of the coil cut any of the field?

Perhaps I am understanding magnetic flux wrong entirely?

Any help would be appreciated.

-Confused A-level student

 

[tiny-tim]

Welcome to PF!

Hi Zatman! Welcome to PF!

If you take a straight wire, the area you take would be the length of the wire times the diameter.

No.

I think you're thinking of the square loop in this hyperphysics diagram.

So why is it that when you coil that wire around the flux changes because you apparently take the area of the circle it describes? How does the empty space in the middle of the coil cut any of the field?

the field lines go through the loop

that's what flux is!

study the links from that hyperphysics page ​

 

[Zatman]

Thanks for the reply, tiny-tim.

I have read your links, but I still don't understand.

I think my problem is more fundamental than that. So how would you calculate the flux for a straight conductor?

As for the coil, my original post might not have been clear, so I made a quick diagram (attached). The ring represents a coil of wire. From what I understand about magnetic flux, the area used should be the blue shaded area - I don't see how the part inside matters because only the wire is cutting the field.

I am sure this is simply because I don't understand what 'flux' really means, I doubt my textbook would make such a mistake.

 

[tiny-tim]

So how would you calculate the flux for a straight conductor?

i don't understand the question

what flux? what is doing what?

… I made a quick diagram (attached). The ring represents a coil of wire. From what I understand about magnetic flux, the area used should be the blue shaded area - I don't see how the part inside matters because only the wire is cutting the field.

the flux looks like zero

can you provide a link to an actual passage in your textbook that you don't understand?​

 

[Zatman]

i don't understand the question

what flux? what is doing what?

Right, so the wire has to be moved for there to be a 'flux'? Then the flux is simply B times the area of the rectangle 'swept' through?

[...]the flux looks like zero

Actually... would this case be zero because current in the wire would not be perpendicular to the field?

What about the new case (attached).
>is there a magnetic flux only when the coil is moved? (I think the answer is "no"?)
>regardless of whether the coil needs to be moved or not, what area do you use?

can you provide a link to an actual passage in your textbook that you don't understand?

Not really; I'm having trouble with the general principle.

 

[tiny-tim]

Right, so the wire has to be moved for there to be a 'flux'? Then the flux is simply B times the area of the rectangle 'swept' through?

that's right …

flux is through an area, not a 1D line …

a moving line sweeps out an area, so we can talk about the flux through that area (usually the rate of change of that flux per time)

Actually... would this case be zero because current in the wire would not be perpendicular to the field?

yes

What about the new case (attached).
>is there a magnetic flux only when the coil is moved? (I think the answer is "no"?)
>regardless of whether the coil needs to be moved or not, what area do you use?

it's an area (not a 1D line), so there's a flux anyway (moving or not)

you use the whole inside area, and you multiply it by the field

(that's assuming the field is constant … if not, the flux is ∫∫ field dxdy)

 

[Zatman]

Good, that made perfect sense until:

that's right …
it's an area (not a 1D line), so there's a flux anyway (moving or not)

you use the whole inside area, and you multiply it by the field

This is what I am having trouble with. Is there any way of explaining, in relatively simple terms, why you use that area -- to me it seems like only the wire is 'cutting' the field, so the field lines that do not pass through the physical wire should not be taken into account.

(that's assuming the field is constant … if not, the flux is ∫∫ field dxdy)

Yes, we only consider uniform constant magnetic fields at A-level.

 

[tiny-tim]

Is there any way of explaining, in relatively simple terms, why you use that area -- to me it seems like only the wire is 'cutting' the field, so the field lines that do not pass through the physical wire should not be taken into account.

think "cookie-cutter"!

 

[Zatman]

think "cookie-cutter"!

Ha, that will suffice I think!

Thanks for your assistance, tiny-tim. Much appreciated.