- #1
lolproe
- 3
- 0
Hi, I'm having a problem with a MATLAB assignment in my probability class. It has to do with finding the joint and marginal PDFs of a pair of random variables. I understand this stuff on paper, but for some reason this assignment is giving me problems since I don't have a good idea of how the random variables translate into a graph.
Here are the two questions giving me troubles
The plot produced by test.m is attached as 1.jpg
Nothing as far as I know beyond basic probability stuff and integration
My main problem is that I don't conceptually understand how to take a graph of sample data points and translate it into a PDF. After looking at the graph for a while, my guess at the joint PDF is
[tex]f(x,y)=\left\{\begin{array}{cc}1-x,&\mbox{ if }
0\leq x\leq y\leq 1\\0, & \mbox{ otherwise } \end{array}\right.[/tex]
It makes sense to me logically, since for a given y value, x can only be as large as the y value and its probability decreases linearly as x increases from 0 to y. So that should cover part a, but I really don't know if I'm right.
For b, I just integrated it over the range of y, so:
[tex]f(x)=\int_x^1 (1-x)dy = (1-x)y|_x^1 =\left\{\begin{array}{cc}(1-x)^2,&\mbox{ if }
0\leq x\leq 1\\0, & \mbox{ otherwise } \end{array}\right.[/tex]
I'm not really good with the limits during this sort of thing, so I figure this is probably where I made a mistake but I'm not sure.
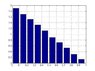
When I run test.m, it saves X as a variable in MATLAB, and I have also have a function which plots the normalized histogram of a chosen variable with a number of bins. So running this script on X with 10 bins, I get the second attachment, 2.jpg.
This is where things really start confusing me. From looking at that, it seems like the marginal PDF should be linear, or specifically [tex]2(1-x)[/tex] instead of [tex](1-x)^2[/tex]. This would be easy to get from my joint PDF, but I see no way to get my Y limits to be as simple as 0 and 2. This is the main problem I have with the question. This is the first chance I have to really verify my work and it doesn't match up, so I don't know where I made my mistake. Any help would be much appreciated, thanks
[edit]
Looking at the question again, I guess it saying the values are uniformly distributed could lead somewhere but I'm not sure how. I tried assuming the marginal PDF was a uniform distribution with y as the limit but that didn't really get me any closer to the answer.
Homework Statement
Here are the two questions giving me troubles
a) Run test.m once. This program generates 10,000 samples of the RV pair (X; Y ) uniformly
distributed over a region. You rst task is to identify the region and guess the PDF. To this end,
get the scatter plot of these samples and come up with an analytical expression for the joint PDF
f(x; y). Note that you need to give the exact denition of f(x; y).
b) Derive the marginal PDF of X by integrating f(x; y) over y. Let us call it f(x). By using
NormHist.m on X, plot the normalized histogram of X and f(x) on the same graph. Comment on
their match.
The plot produced by test.m is attached as 1.jpg
Homework Equations
Nothing as far as I know beyond basic probability stuff and integration
The Attempt at a Solution
My main problem is that I don't conceptually understand how to take a graph of sample data points and translate it into a PDF. After looking at the graph for a while, my guess at the joint PDF is
[tex]f(x,y)=\left\{\begin{array}{cc}1-x,&\mbox{ if }
0\leq x\leq y\leq 1\\0, & \mbox{ otherwise } \end{array}\right.[/tex]
It makes sense to me logically, since for a given y value, x can only be as large as the y value and its probability decreases linearly as x increases from 0 to y. So that should cover part a, but I really don't know if I'm right.
For b, I just integrated it over the range of y, so:
[tex]f(x)=\int_x^1 (1-x)dy = (1-x)y|_x^1 =\left\{\begin{array}{cc}(1-x)^2,&\mbox{ if }
0\leq x\leq 1\\0, & \mbox{ otherwise } \end{array}\right.[/tex]
I'm not really good with the limits during this sort of thing, so I figure this is probably where I made a mistake but I'm not sure.
When I run test.m, it saves X as a variable in MATLAB, and I have also have a function which plots the normalized histogram of a chosen variable with a number of bins. So running this script on X with 10 bins, I get the second attachment, 2.jpg.
This is where things really start confusing me. From looking at that, it seems like the marginal PDF should be linear, or specifically [tex]2(1-x)[/tex] instead of [tex](1-x)^2[/tex]. This would be easy to get from my joint PDF, but I see no way to get my Y limits to be as simple as 0 and 2. This is the main problem I have with the question. This is the first chance I have to really verify my work and it doesn't match up, so I don't know where I made my mistake. Any help would be much appreciated, thanks
[edit]
Looking at the question again, I guess it saying the values are uniformly distributed could lead somewhere but I'm not sure how. I tried assuming the marginal PDF was a uniform distribution with y as the limit but that didn't really get me any closer to the answer.
Attachments
Last edited: