Projectile Motion: How to Calculate Initial Velocity for a Golf Shot

  • Thread starter Thread starter smashbrohamme
  • Start date Start date
  • Tags Tags
    Projectile
AI Thread Summary
To calculate the initial velocity for a golf shot that travels 130 meters horizontally and lands 10 meters below the tee-off point, the golfer must first determine the vertical component of the initial velocity and the time it takes for the ball to reach the target height. The vertical acceleration is -9.81 m/s², and the initial vertical velocity is calculated to be 19.8 m/s, with a time of 2 seconds for the ascent. The next step involves finding the horizontal component of the initial velocity using the time calculated for the vertical motion. The final answer for the initial velocity is 35.1 m/s at an angle of 34.4 degrees. Understanding the relationships between the components of motion is crucial for solving the problem.
smashbrohamme
Messages
97
Reaction score
1
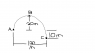
A golfer wants to hit the ball a horizontal distance of 130M and 20M above his tee-off point, but wants the ball to land 10 M below his tee-off point. What is the balls Initial velocity?


S= VoT+1/2AT²
V= Vo+AT
V²=Vo²+2AS

So far I have broken up the graph into 3 Parts...from Point A to Point B i have solved for the Y direction.
Ay= -9.81m/s²
Voy= 19.8m/s
Vx= 0
Sy= 20m
T= 2s

But I can't seem to start off in the X direction...do I go from Point A to C? B to C in the Y direction? I am really lost everytime I try to solve another direction from ethier point I have no information to create a solution.

btw the answer is Vo= 35.1 m/s angled at 34.4 so please just help me from understanding how to go from here.
 

Attachments

  • Projectile problem.png
    Projectile problem.png
    5.4 KB · Views: 438
Physics news on Phys.org
You must do things in this order: determine the Y component of initial velocity, determine the time for the ball to reach C, determine the X component of the initial velocity using the time.

What part of these three steps are you struggling with?
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Projectile Motion Problem Involving Initial Velocity and Gravity Only
Replies
11
Views
1K
Projectile Motion: golf ball velocity to reach the green
Replies
11
Views
4K
What Calculations Determine the Volleyball's Trajectory in Projectile Motion?
Replies
33
Views
4K
Understanding Projectiles (Example Problem Given)
Replies
1
Views
2K
Golf club 🏌️and ball ⛳ impulse problem
Replies
19
Views
2K
Projectile Motion - vertical displacement at specific time.
Replies
3
Views
2K
How Do You Solve a Projectile Motion Problem?
Replies
3
Views
4K
Projectile Motion of football receiver
Replies
9
Views
4K
Projectile Motion: Finding the Maximum Height of a Football
Replies
5
Views
6K
Projectile Motion Practice Problems | Calculate Distance and Maximum Height
Replies
8
Views
4K

Hot Threads

Recent Insights

Back
Top