MHB Projectile Motion Lab: Solving Equations with Newton's Law and Experimental Data

[Alelin]

Hi there
I need help with my lab to solve motion equations using Newtons law
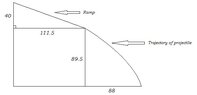
Basically I did my experiment based in projectile motion, one of the trial give me 88cm out of the ramp, like distance traveled, then the total horizontal length of the ramp was 111.5cm and the height 40cm, also the vertical height of the ramp before touching ground was 89.5, I'm pretty stuck looking for displacement and time, if you can help me I will be kindly greatful(Sun)

 

[MarkFL]

Just so we understand correctly, I am assuming a projectile, likely a small ball, is rolled down a ramp, and then free falls 89.5 cm down to the ground, as in the following diagram, where the measures are in cm:

View attachment 1236

The projectile hits the ground a horizontal distance of 88 cm from the bottom end of the ramp. Is this correct?

 

[Alelin]

Just so we understand correctly, I am assuming a projectile, likely a small ball, is rolled down a ramp, and then free falls 89.5 cm down to the ground, as in the following diagram, where the measures are in cm:

View attachment 1236

The projectile hits the ground a horizontal distance of 88 cm from the bottom end of the ramp. Is this correct?

yes that is exactly what I meant, hehehe you got it, but how I'm suppose to get the displacement and time?

 

[MarkFL]

I would begin with the parametric equations of motion:

(1) $$x=v_0\cos(\theta)t$$

(2) $$y=-\frac{g}{2}t^2+v_0\sin(\theta)t$$

To eliminate the parameter $t$, we solve (1) for $t$ and substitute into (2) to get:

(3) $$y=\tan(\theta)x-\frac{g}{2v_0^2\cos^2(\theta)}x^2$$

Now we have the height $y$ of the ball as a function of the initial velocity $v_0$, the launch angle $\theta$ and the horizontal displacement $x$. Be sure to convert all of the measures to meters, since $g$ uses the meter in its units.

Are you supposed to consider the moment of inertia of the ball, or are you to treat it like a particle?

Do you know how to find the velocity of the projectile just as it leaves the ramp?

I would use the equation:

$$v_0=\sqrt{2a\ell}$$

where:

$\ell$ is the length of the inclined portion of the ramp, i.e., the distance through which the projectile is accelerated before free falling. Use the Pythagorean theorem to find it, since it is the hypotenuse of a right triangle and you know the leg lengths.

$a$ is the acceleration of the projectile as it moves down the ramp. This will be a function of $g$, the acceleration due to gravity, the vertical component of the ramp's inclination, and the length of the ramp $\ell$, hence you should verify that we find:

$$a=g\frac{0.40}{\ell}$$

Once you have $v_0$, and $\theta$ (the negative of the angle of inclination of the ramp), you may use (1) and(2) to parametrically describe the trajectory of the projectile.

 

[Alelin]

Sorry Mark already got the Hypotenuse should be 111.5 and the opposite is 40 therefore is 21 degrees, but how I should get the cos angle?

 

[MarkFL]

Oh, okay, so the hypotenuse is 111.5 cm, then the side opposite the angle is 40 cm. Use the Pythagorean theorem to get the side adjacent to the angle, we'll call it $x$, and we may write:

$$x^2+40^2=111.5^2$$

Now solve for $x$, and then:

$$\cos(\alpha)=\frac{2x}{223}$$

As far as the angle of inclination $\alpha$ of the ramp, I would use:

$$\alpha=\sin^{-1}\left(\frac{80}{223} \right)$$

for all intermediary calculations, and only do your rounding at the very end. This is what I was taught to do when carrying out physics experiments. :D

 

[Alelin]

Oh, okay, so the hypotenuse is 111.5 cm, then the side opposite the angle is 40 cm. Use the Pythagorean theorem to get the side adjacent to the angle, we'll call it $x$, and we may write:

$$x^2+40^2=111.5^2$$

Now solve for $x$, and then:

$$\cos(\alpha)=\frac{2x}{223}$$

As far as the angle of inclination $\alpha$ of the ramp, I would use:

$$\alpha=\sin^{-1}\left(\frac{80}{223} \right)$$

for all intermediary calculations, and only do your rounding at the very end. This is what I was taught to do when carrying out physics experiments. :D

Im trying to do your way but I am not sure how do you got that 223 and also can you tell me how I can plug it in my results in a graph on excel using x and y scatter

 

[MarkFL]

The 223 comes from doubling 111.5 so that our ratios have integers in them.

Have you determined $\theta$ and $v_0$?

 

[Alelin]

The 223 comes from doubling 111.5 so that our ratios have integers in them.

Have you determined $\theta$ and $v_0$?

well if I put sin-1= 0.40/1.115= 21'

but the initial velocity give me a weird number like 0.40sin21= 0.14... I don't think that is correct

 

[MarkFL]

Yes, that is incorrect...

Recall:

$$v_0=\sqrt{2a\ell}$$

where:

$$a=g\frac{0.4}{\ell}$$

and so:

$$v_0=\sqrt{2\left(g\frac{0.4}{\ell} \right)\ell}=\sqrt{0.8g}=2\sqrt{\frac{g}{5}}$$

Also recall:

$$\theta=-\alpha=-\sin^{-1}\left(\frac{80}{223} \right)$$

And so, to find the time the projectile was falling, use:

$$x=v_0\cos(\theta)t\implies t=\frac{x}{v_0\cos(\theta)}$$

where $x=0.88\text{ m}$.

What do you find?

 

[Alelin]

Yes, that is incorrect...

Recall:

$$v_0=\sqrt{2a\ell}$$

where:

$$a=g\frac{0.4}{\ell}$$

and so:

$$v_0=\sqrt{2\left(g\frac{0.4}{\ell} \right)\ell}=\sqrt{0.8g}=2\sqrt{\frac{g}{5}}$$

Also recall:

$$\theta=-\alpha=-\sin^{-1}\left(\frac{80}{223} \right)$$

And so, to find the time the projectile was falling, use:

$$x=v_0\cos(\theta)t\implies t=\frac{x}{v_0\cos(\theta)}$$

where $x=0.88\text{ m}$.

What do you find?

Time? like 1.30
I'm so over of this I have to finish the report for tomorrow and this calculation to plug it in the results on the graph is taking ages! but thanks for your patience and tuition it made it easier hopefully I can do a graph at least, but thank you again

 

[MarkFL]

No, you should write:

$$t=\frac{0.88\text{ m}}{2\sqrt{\frac{g}{5}}\frac{\text{m}}{\text{s}} \cos\left(-\sin^{-1}\left(\frac{80}{223} \right) \right)}$$

Using $g=9.8$ (or a more accurate value if so instructed), what do you get?

 

[Alelin]

No, you should write:

$$t=\frac{0.88\text{ m}}{2\sqrt{\frac{g}{5}}\frac{\text{m}}{\text{s}} \cos\left(-\sin^{-1}\left(\frac{80}{223} \right) \right)}$$

Using $g=9.8$ (or a more accurate value if so instructed), what do you get?

I got 0.8049... but that way to solve the problem goes beyond my syllabus we where taught with different formulas and therefore I'm getting different results all the time

 

[MarkFL]

Using my calculator, I find:

$$t\approx0.336697716407181\text{ s}$$

Is your calculator in radian mode?

I can only guess what you are given or are expected to use.

What exactly are you supposed to be finding? I suspect it is more than just the time the projectile is in the air.

 

[sweer6]

I think this physics-math website will have answers to your question with very good explanations
Trajectories