Projectile Motion on a sloped surface

In summary, a projectile is launched at 10m/s from a 30 degree angled surface at a 45 degree angle relative to the horizon. The task is to find the distance from the launching point where the projectile lands and the time it takes to reach this point. The equations used are v = 10 m/s for the initial velocity and projectile motion equations to derive the parabola and sloped surface. The solution involves finding the intersection of these equations. The dimensions are not given and should be derived from the equations, not guessed from the diagram.
  • #1
Doonami
5
0

Homework Statement


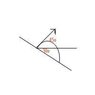
A projectile is launched at 10m/s from a sloped surface. The surface is angled 30degrees, and the projectile is launched off from the surface at a 45degrees angle relative to the horizon.

Find the distance from the launching point where the projectile lands.
How long does it take to reach this point?

Homework Equations


v = 10 m/s

The Attempt at a Solution


I've tried solving this by resolving the angled plane as the horizon, giving the projectile angled at 75degrees, but I don't think this is the right way to proceed, the parabolic shape would not be preserved by this, and the length from origin would be wrong.

Thanks for the help, I'm really struggling how to approach this problem.
 

Attachments

  • physics1.jpg
    physics1.jpg
    1.8 KB · Views: 556
Physics news on Phys.org
  • #2
Can you come up with an equation describing the parabola? And one describing the sloped surface? Find their intersection.
 
  • #3
I considered that as well. However no dimensions are given. The picture provided is almost exactly as it was presented.
 
  • #4
Doonami said:
However no dimensions are given. The picture provided is almost exactly as it was presented.
Don't try to guess it off the diagram. Derive it from projectile motion equations.
 

FAQ: Projectile Motion on a sloped surface

What is projectile motion on a sloped surface?

Projectile motion on a sloped surface is the movement of an object that is thrown or launched on an incline. This type of motion is influenced by both gravity and the angle of the slope, resulting in a curved path.

How does the angle of the slope affect projectile motion?

The angle of the slope has a significant impact on projectile motion. A steeper slope will result in a faster and shorter trajectory, while a shallower slope will result in a slower and longer trajectory. The angle also affects the height and distance the object will travel.

What is the difference between horizontal and vertical components in projectile motion on a sloped surface?

The horizontal component of projectile motion refers to the object's motion along the slope, while the vertical component refers to the object's motion perpendicular to the slope. The horizontal component is affected by the initial velocity and the angle of the slope, while the vertical component is affected by gravity.

How can we calculate the range of a projectile on a sloped surface?

The range of a projectile on a sloped surface can be calculated using the formula R = (v²/g) * sin(2θ), where R is the range, v is the initial velocity, g is the acceleration due to gravity, and θ is the angle of the slope. This formula assumes that the slope is frictionless and the object is launched from ground level.

What are some real-life applications of projectile motion on a sloped surface?

Projectile motion on a sloped surface is commonly used in sports such as skiing, snowboarding, and skateboarding. It is also applied in engineering, specifically in the design of roller coasters and other amusement park rides. Additionally, the concept of projectile motion on a sloped surface is used in physics experiments and demonstrations to study the effects of gravity and angle on an object's trajectory.

Similar threads

I need opinions on a Projectile Motion problem that I made up
Replies
11
Views
1K
Calculate the displacement? (Projectile motion problem)
Replies
3
Views
2K
Projectile motion of a cannon ball versus time
Replies
15
Views
2K
Relationship between Launch height and range of a projectile
Replies
15
Views
23K
How Do You Solve a Projectile Motion Problem?
Replies
3
Views
4K
Where on the hill does the projectile land?
Replies
9
Views
3K
Exploring the Acceleration of a Projectile Motion Lab
Replies
8
Views
2K
Conceptual Question on Projectile Motion
Replies
2
Views
2K
Projectile Motion - object that is shot at an angle of 55 degrees
Replies
8
Views
2K
How Long to Reach Maximum Height for a 70 m/s Projectile at 45 Degrees?
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top