Melawrghk
- 140
- 0
Projectile motion problem - SOLVED
This is one of the last parts of a bigger problem, but I get the first parts. So:
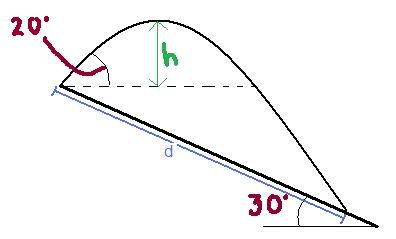
The projectile motion describes a skier's jump. The initial velocity is 21.469m/s at 20 degrees to the horizontal. Find the maximum height the skier reaches (relative to the take off point), find distance 'd' down the slope where the skier lands.
First I wrote the equations:
Vx = 21.469cos(20)
Vy= 21.469sin(20)-gt
Then, I found the time it took for the skier to reach the top:
Vy=21.469sin(20)-9.81t
9.81t=21.469sin(20)
t= 0.7485 seconds
Then I found the 'h':
ds/dt = 21.469sin(20)-9.81t
*integrating...*
s=21.469sin(20)t-4.905t2
s(0.7485) = 2.7481 m
Then I drew this:
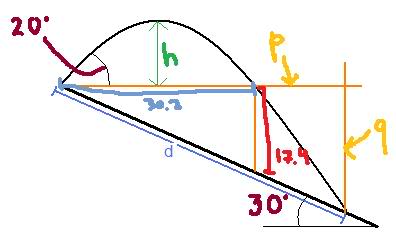
On it, I calculated the 30.2 value by plugging in 0.7485*2 into an x-direction distance equation:
Sx = 0.7485*2 x 21.469cos20 = 30.2
I then found the 17.44 using just trig.
So now, I started to treat the big triangle (described by p and q) as a similar triangle with sides 30.2&17.44 and developed a relationship:
q/p = 17.44/30.2
q=0.577p
Next, I expressed d in terms of p and q:
d2=p2+q2
d2= 1.3329p2
and thus, p=0.866d
I performed similar operations and got:
q=0.5d
Then time for the skier to go the whole horizontal distance:
0.886d = 21.469cos(20)*t
t=0.04293d
And thus the time it will take for the skier to hit the ground from her highest point is:
t=0.0429d-0.7485
Now, we can plug in that equation into the equation of vertical distance travelled:
h+0.5d = 21.469sin(20)(0.0429d-0.7485)-4.905(0.04293d-0.7485)2
I can simplify that and try to find d (from discriminant and things) but I end up with a negative discriminant... Help?
Homework Statement
This is one of the last parts of a bigger problem, but I get the first parts. So:
The projectile motion describes a skier's jump. The initial velocity is 21.469m/s at 20 degrees to the horizontal. Find the maximum height the skier reaches (relative to the take off point), find distance 'd' down the slope where the skier lands.
The Attempt at a Solution
First I wrote the equations:
Vx = 21.469cos(20)
Vy= 21.469sin(20)-gt
Then, I found the time it took for the skier to reach the top:
Vy=21.469sin(20)-9.81t
9.81t=21.469sin(20)
t= 0.7485 seconds
Then I found the 'h':
ds/dt = 21.469sin(20)-9.81t
*integrating...*
s=21.469sin(20)t-4.905t2
s(0.7485) = 2.7481 m
Then I drew this:
On it, I calculated the 30.2 value by plugging in 0.7485*2 into an x-direction distance equation:
Sx = 0.7485*2 x 21.469cos20 = 30.2
I then found the 17.44 using just trig.
So now, I started to treat the big triangle (described by p and q) as a similar triangle with sides 30.2&17.44 and developed a relationship:
q/p = 17.44/30.2
q=0.577p
Next, I expressed d in terms of p and q:
d2=p2+q2
d2= 1.3329p2
and thus, p=0.866d
I performed similar operations and got:
q=0.5d
Then time for the skier to go the whole horizontal distance:
0.886d = 21.469cos(20)*t
t=0.04293d
And thus the time it will take for the skier to hit the ground from her highest point is:
t=0.0429d-0.7485
Now, we can plug in that equation into the equation of vertical distance travelled:
h+0.5d = 21.469sin(20)(0.0429d-0.7485)-4.905(0.04293d-0.7485)2
I can simplify that and try to find d (from discriminant and things) but I end up with a negative discriminant... Help?
Last edited: