mihir23
- 2
- 0
Homework Statement
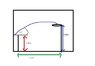
A basketball shoots a ball at an angle of 55° which is 4.3m away( horizontal dist). If the ball is released from a height of 2.1m and lands in the hoop, which is 3m high. Calculate the initial speed of the ball for this shot to be successful.
Homework Equations
initial horiz velocity = v cos(θ)
initial vert velocity = v sin(θ)
Resultant initial velocity = Sqroot(initial horiz v ^2 + initial vert v^2)
The Attempt at a Solution
I decided that the vertical displacement the ball travels is 0.9 m up(3-2.1m)
The question does not give the max height , so i was confused about how to approach it
What i did:
a = -9.8
u= ?
v^2 =u^2 +2as
u^2 =17.64
initial vert velocity = v sin(θ)
therefore
v(initial vert) = 4.2/sin 55
4.2 = v sin 55
= 5.127
v(initial horiz)=5.127/tan55
=3.59
total initial v = Sqroot(5.127^2 + 3.6^2)
=6.26 m/s
This answer is wrong according to the back of my book. Could you please tell me how i have done it incorrectly. If you guys really want it, then i'll post the book's answer.