Simone Furcas
- 10
- 0
Let r:R2 →R3 be given by the formula
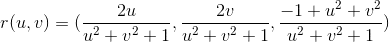 Compute the second fundamental form with respect to this basis (Hint: There’s a shortcut to computing the unit normal n).
Compute the second fundamental form with respect to this basis (Hint: There’s a shortcut to computing the unit normal n).
I can't find thi shortcut, does anyone help me? I'm solving it with normal vector and first and second derivate, but I obtained impossibile result... The solve is too long to write down here... I use I used
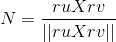
I can't find thi shortcut, does anyone help me? I'm solving it with normal vector and first and second derivate, but I obtained impossibile result... The solve is too long to write down here... I use I used