B Proof of Cyclic Quadrilateral AEDT in Circle ABCD

[lungoy]

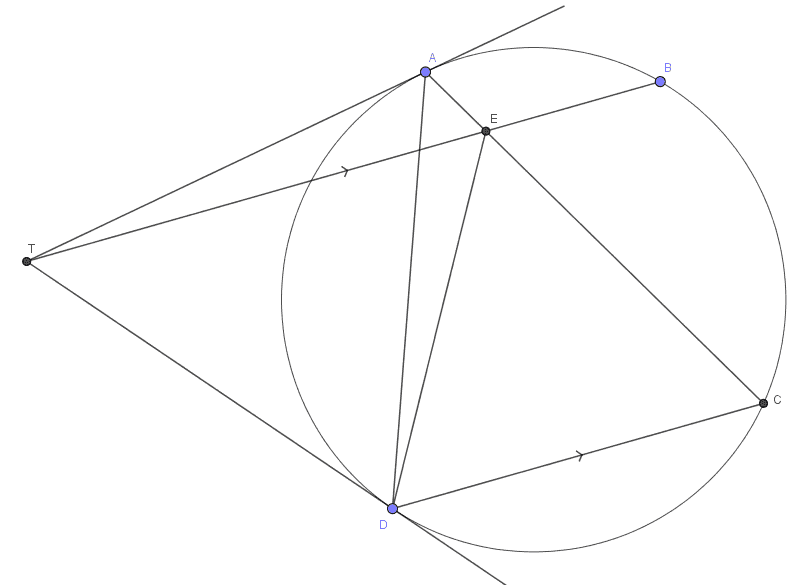
$TA$ and $TD$ are tangent line of circle $ABCD$ and $TB \parallel DC$. Show $A,E,D,T$ are cyclic quadrilateral.
I know $x=\angle TAD= \angle TDA = \angle ACD= \angle TEA$
And $\angle ATD=180-2x$
But I don't know how to prove $\angle AED=x$.
Or there's another easily method?
Thanks.

 

[lungoy]

I've just known that $\angle TEA = \angle TDA$ prove $AEDT$ are cyclic.
The problem is solved. Thanks.