daniel123
- 2
- 0
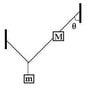
In my Physics 231 class (Calculus Based) I was given a homework problem asking me to prove the following equation. It had a picture attached but the equation was:
Tan (theta) = 1 + (2M / m)
The two (m) represent different masses balanced in equilibrium while hanging with 3 tension forces none of which are connected to the other mass. If you need anymore information just post what you need below. Thank you.
|
/ |
/ |
| / (theta)
| /__________
| \ M
\ /
\ /
45 Degrees \ / 45 Degrees
______|______
|
m
Tan (theta) = 1 + (2M / m)
The two (m) represent different masses balanced in equilibrium while hanging with 3 tension forces none of which are connected to the other mass. If you need anymore information just post what you need below. Thank you.
|
/ |
/ |
| / (theta)
| /__________
| \ M
\ /
\ /
45 Degrees \ / 45 Degrees
______|______
|
m