Prooving a system will travel up to 180 degrees

AI Thread Summary
The discussion revolves around proving that a system can rotate freely up to 180 degrees, involving a counterweight (m2) and a mass (m1) of a pan. Users are seeking clarification on the equations provided, particularly the right-hand side of the equation, which is causing confusion regarding its components and meaning. There are questions about the diagram's clarity, the definition of terms like "pan" and "bearing housing," and the pivot point of the system. Participants are trying to understand the relationships between the forces and the geometry of the setup to validate the proof. Overall, the conversation highlights the need for clearer definitions and better visual aids to facilitate understanding of the mechanics involved.
physicsodyssey
Messages
11
Reaction score
6

Homework Statement


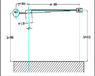
To prove that system will travel freely upto 180 degree
m2 is counterweight and m1 is mass of pan (=3kg)
i have attched the fbd or another link http://www.imagebam.com/image/54bb5a394377595

Homework Equations


m1(h + a sin θ) g x = m2 y h g
m2 = 9.13 kg

The Attempt at a Solution


we are stuck at the following equation
Pwg ≥( m1 x^2 + m2 y^2) sin2 θ / [ x(h-xsin2 θ)]
LHS is weight of pan and arm and if LHS>RHS, system will rotate freely
is this correct? can you pls explain it properly because it will clear my concepts.
Thanks.
 

Attachments

  • fzg.PNG
    fzg.PNG
    6.7 KB · Views: 523
Physics news on Phys.org
Hello, welcome to PF :smile:

Could you clarify the problem statement a bit more? The diagram is difficult to read, I see no forces, what is what, what is the pivot point, what is a, what is P w (pr Pw ?), etc.
 
a is the length of bearing housing(the middle block which is the reference axis) hence a sin θ is added to h for balancing. my issue is the second equation. i cannot understand the RHS side.LHS is simply the wt of pan and tray.(ρwg).
can you help me with the equation on RHS
( m1 x^2 + m2 y^2) sin2 θ / [ x(h-xsin2 θ)]
Thanks a lot for a warm welcome in this wonderful community.
 
Still lost -- or rather not "in":

The thing on the right is a pan. What is a pan ? The thing in the middle is a bearing housing. Interesting. Does it pivot around some axis ? What axis ?

If the LHS was the weight of the pan and arm and now is the weight of the pan and tray, how come m1 doesn't feature in it ? What tray ?
What is s ?

What does the equation m1(h + a sin θ) g x = m2 y h g represent ? I see something in kg m3 /s2

What is ##\theta## ? What's the blue horizontal line ? And the black sloping line just underneath ?

THe fat black lines to L and R ? The thin black lines (where the h are mentionsed) ?

What is dangling from the bearing housing ? Where is the reference point for a ?

Are lengths measured in meters ?

What has to rotate 180 degrees ? Doesn't it bum into the fat line on the left ?
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

System of two pulleys and three masses
Replies
22
Views
6K

Hot Threads

Recent Insights

Back
Top