Proper Subsets of Ordinals .... .... Searcoid, Theorem 1.4.4 .

In summary, the conversation discusses a question about Theorem 1.4.4 in Michael Searcoid's book "Elements of Abstract Analysis". Specifically, the question pertains to the proof given by Searcoid and how the minimality of ##\beta## with respect to ##\in## in ##\alpha \text{\\} x## ensures that ##\gamma## belongs to ##x##. The conversation also mentions the definitions of well order and ordinals given by Searcoid. The question is eventually answered, with Andrew clarifying that the argument is based on the fact that if ##\gamma## is less than ##\beta##, then ##\beta## cannot be the least element of
  • #1
Math Amateur
Gold Member
MHB
3,990
48
I am reading Micheal Searcoid's book: "Elements of Abstract Analysis" ... ...

I am currently focused on understanding Chapter 1: Sets ... and in particular Section 1.4 Ordinals ...

I need some help in fully understanding Theorem 1.4.4 ...

Theorem 1.4.4 reads as follows:
?temp_hash=4bda424fad298c1e9971999ab230fc84.png


In the above proof by Searcoid we read the following:

"... ... Now, for each ##\gamma \in \beta## , we have ##\gamma \in \alpha## by 1.4.2, and the minimality with respect to ##\in## of ##\beta## in ##\alpha \text{\\} x## ensures that ##\gamma \in x##. ... ...Ca someone please show formally and rigorously that the minimality with respect to ##\in## of ##\beta## in ##\alpha \text{\\} x## ensures that ##\gamma \in x##. ... ...

*** EDIT ***

Is the argument simply that since ##\beta## is the least element of ##\alpha \text{\\} x## ... then if ##\gamma \in \beta## ... then ##\gamma## cannot belong to ##\alpha \text{\\} x## ... otherwise ##\gamma## would be the least element ... and so ##\gamma## must belong to ##x## ...

*** *** ***Help will be appreciated ...

Peter

==========================================================================It may help Physics Forum readers of the above post to have access to the start of Searcoid's section on the ordinals (including Theorem 1.4.2 ... ) ... so I am providing the same ... as follows:
?temp_hash=4bda424fad298c1e9971999ab230fc84.png


It may also help Physics Forum readers to have access to Searcoid's definition of a well order ... so I am providing the text of Searcoid's Definition 1.3.10 ... as follows:

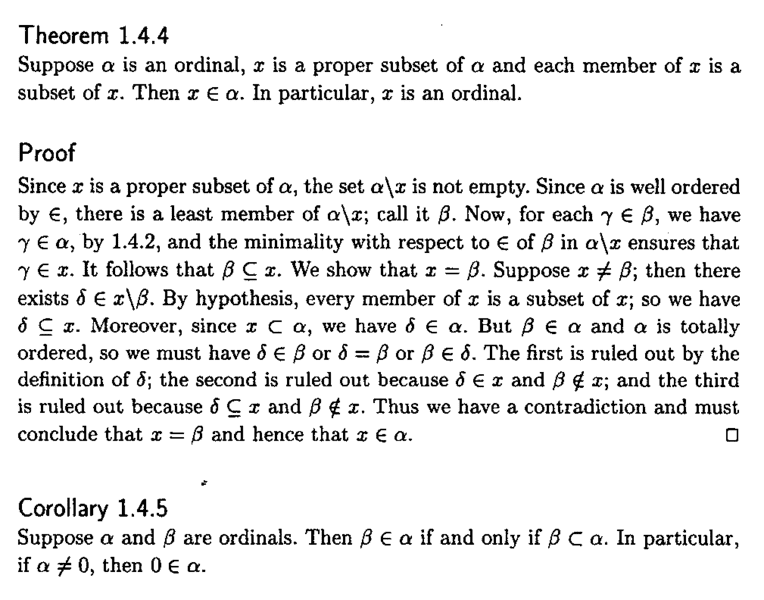
?temp_hash=4bda424fad298c1e9971999ab230fc84.png

?temp_hash=4bda424fad298c1e9971999ab230fc84.png

Hope that helps ...

Peter
 

Attachments

  • Searcoid - Theorem 1.4.4 ... ....png
    Searcoid - Theorem 1.4.4 ... ....png
    44.9 KB · Views: 500
  • Searcoid - 1 - Start of section on Ordinals ... ... PART 1 ... .....png
    Searcoid - 1 - Start of section on Ordinals ... ... PART 1 ... .....png
    31.4 KB · Views: 429
  • Searcoid - Definition 1.3.10 ... .....png
    Searcoid - Definition 1.3.10 ... .....png
    24.8 KB · Views: 426
  • Searcoid - 2 - Definition 1.3.10 ... .....PART 2 ... ....png
    Searcoid - 2 - Definition 1.3.10 ... .....PART 2 ... ....png
    25.6 KB · Views: 422
  • Searcoid - 2 - Definition 1.3.10 ... .....PART 2 ... ....png
    Searcoid - 2 - Definition 1.3.10 ... .....PART 2 ... ....png
    25.6 KB · Views: 329
  • ?temp_hash=4bda424fad298c1e9971999ab230fc84.png
    ?temp_hash=4bda424fad298c1e9971999ab230fc84.png
    44.9 KB · Views: 437
  • ?temp_hash=4bda424fad298c1e9971999ab230fc84.png
    ?temp_hash=4bda424fad298c1e9971999ab230fc84.png
    31.4 KB · Views: 408
  • ?temp_hash=4bda424fad298c1e9971999ab230fc84.png
    ?temp_hash=4bda424fad298c1e9971999ab230fc84.png
    24.8 KB · Views: 396
  • ?temp_hash=4bda424fad298c1e9971999ab230fc84.png
    ?temp_hash=4bda424fad298c1e9971999ab230fc84.png
    25.6 KB · Views: 415
Last edited:
Physics news on Phys.org
  • #2
Math Amateur said:
Is the argument simply that since ##\beta## is the least element of ##\alpha \text{\\} x## ... then if ##\gamma \in \beta## ... then ##\gamma## cannot belong to ##\alpha \text{\\} x## ... otherwise ##\gamma## would be the least element ... and so ##\gamma## must belong to ##x## ...
Almost. Just replace '##\gamma## would be the least element' by '##\gamma## would be less than ##\beta##, so ##\beta## could not be the least element'
 
  • Like
Likes Math Amateur
  • #3
Thanks Andrew ...

Appreciate your help ...

Peter
 

What are proper subsets of ordinals?

Proper subsets of ordinals refer to sets that contain only a subset of the elements of a given ordinal set. In other words, the proper subset does not contain all the elements of the original set.

What is the significance of Theorem 1.4.4 in Searcoid's work?

Theorem 1.4.4 in Searcoid's work states that every ordinal can be written uniquely as a sum of a limit ordinal and a successor ordinal. This theorem is significant because it provides a way to classify and understand different types of ordinals.

How do proper subsets of ordinals relate to the concept of infinity?

Proper subsets of ordinals are important in the study of infinity because they help us understand the different levels of infinity. Each proper subset represents a smaller level of infinity, while the original ordinal set represents the largest level of infinity.

Can proper subsets of ordinals be compared to each other?

Yes, proper subsets of ordinals can be compared using the concept of order. If one proper subset is a subset of another proper subset, then the larger proper subset is considered to be greater in order than the smaller proper subset.

What is the practical application of studying proper subsets of ordinals?

The study of proper subsets of ordinals has practical applications in fields such as computer science and set theory. It helps us understand the structure and properties of infinite sets, which are important in many areas of mathematics and science.

Similar threads

I Ordinals .... Searcoid, Corollary 1.4.5 .... ....
    • Topology and Analysis
Replies
4
Views
1K
I Proper Subsets of Ordinals .... .... Another Question .... ....
    • Topology and Analysis
Replies
2
Views
1K
I Ordinals .... Searcoid, Theorem 1.4.6 .
    • Topology and Analysis
Replies
2
Views
1K
I Properties of the Ordinals ....
    • Topology and Analysis
Replies
2
Views
1K
MHB Proper Subsets of Ordinals .... .... Searcoid, Theorem 1.4.4 .... ....
    • Set Theory, Logic, Probability, Statistics
Replies
1
Views
829
I The Order Topology .... .... Singh, Example 1.4.4 .... ....
    • Topology and Analysis
Replies
2
Views
2K
MHB Ordinals .... Searcoid, Corollary 1.4.5 .... ....
    • Set Theory, Logic, Probability, Statistics
Replies
1
Views
966
I Help with basic transfinite induction proof
    • Topology and Analysis
Replies
2
Views
151
MHB Understanding Proper Subsets of Ordinals in Searcoid's Theorem 1.4.4 - Peter
    • Set Theory, Logic, Probability, Statistics
Replies
2
Views
996
MHB Ordinals .... Searcoid, Theorem 1.4.6 ....
    • Set Theory, Logic, Probability, Statistics
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top