anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
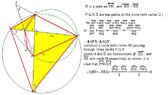
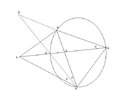
Let $A$ be the intersection point of the diagonals $PR$ and $QS$ of a convex quadrilateral $PQRS$. The bisector of angle $PRS$ hits the line $QP$ at $B$. If $AP\cdot AR+AP\cdot RS=AQ\cdot AS$, prove that $\angle QBR=\angle RSQ$.