Prove: angular momentum is preserved

[Gbox]

Homework Statement

A particle of mass $m$ is moving in a central field with potential $V(r)$ the lagrangian in Spherical coordinate is $l=\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2+r^2sin^2\theta\dot{\phi}^2)-V(r)$

Relevant Equations

$P_i=\frac{\partial }{(\partial \dot{p}_i )}$

$H(p,q)=\sum_(i=1)^n(p_i\cdot \dot{r}_i)-L$

$\dot{q}=\frac{\partial H}{(\partial p_i )}$

$\dot{p}_i=\frac{-\partial H}{(\partial q_i }$

3. Find the hamilton equations
4. using 3. prove the the angular momentum in the z axis $L_z=m(x\dot y-xy\dot)$ is preserved.

I got in $3$:

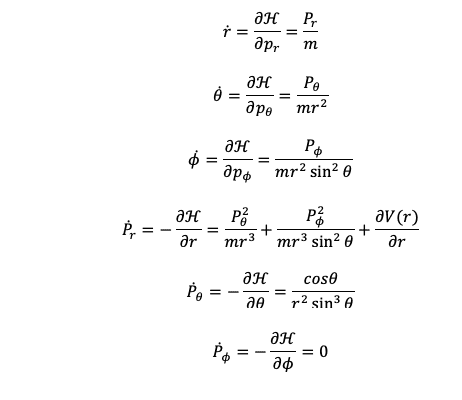
How can I prove 4?

 

[PeroK]

The key equation is $\dot{P_{\phi}} = 0$ as that represents a conservation law.

You also have an equation for $P_{\phi}$ there. Can you show that is equal to $L_z$?

 

[Gbox]

The key equation is $\dot{P_{\phi}} = 0$ as that represents a conservation law.

You also have an equation for $P_{\phi}$ there. Can you show that is equal to $L_z$?

Do you mean
$-\frac{\partial H}{\partial \phi}=m(x\dot{y}-y\dot{x})$

Where $x=rsin\theta cos\phi, y=rsin\theta sin\phi$?

 

[PeroK]

Do you mean
$-\frac{\partial H}{\partial \phi}=m(x\dot{y}-y\dot{x})$

Where $x=rsin\theta cos\phi, y=rsin\theta sin\phi$?

I mean your third equation below.

View attachment 245209