The proof cannot be made with integrals, because a random surface haven't a defined functional form.
The below proof is geometric and more than enough to convince the reader.
.
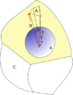
Imagine any convex surface
C and any point
P inside it. Now imagine a sphere
s of radius
r totally contained in the closed surface that has as its center the reference point
P. Now get a microcone from a piece of the surface closed in
C (Area
A) with the vertex in the center (
P). It crosses the inner sphere in area
a. The microcone is small enough to approximate the piece in
C by a small piece of a sphere of radius
R with
P center.
Thus the microcones are similar and it is obvious that the solid angle is the same. (
A / R2 = a /r2). If we extended the sphere of radius
R and get all the cones, we would reach the same
4π. When we take the next microcone from the outer surface, the larger radius would change, but in the same way we could associate with the angle of the inner sphere. So when we go through the entire outer surface exhaustively, we will reach the same
4π.
How to ensure that the smaller sphere will not have holes or overlaps? Holes are impossible because the extension of the smaller sphere must cross the closed surface. overlaps are impossible because the segment starting from P crosses the closed surface only once before leaving the closed convex surface.
Rigorously, there is a problem in the proof, because in fact the solid angle is the scalar product between the vector unit radius and the a vector normal to the surface with module area, divided by the square of the radius
R, which turns to
A cos θ / R2. However, there is no problem because everything happens as if considering the microarea in
C perpendicular to the radius
R, multiplying by the
cos θ. This does not change the opening of the angle.
For any external point
P the same solid angle would give 0 in relation to a convex surface C:
A small sphere around
P is also constructed. Every microcone crossing the sphere
s toward
P would cross surface
C twice, one entering and the other leaving. When it comes in, the solid angle is negative (opposite to normal array outside surface) and when it leaves the surface, it is negative. By similar reasoning, it is seen that the angle module is the same on the small sphere, so the values are always canceled.
All that has been said above is valid for non-convex surfaces. When
P is inside, the difference is that the number of crosses with
s is odd, half entering and half leaving and one more leaving. Thus all are canceled, less the last one, reducing to the proof that already has been made. When
P is outside the surface, the number of crosses is always even, half entering and half leaving, all canceling out.