r0bHadz
- 194
- 17
Homework Statement
Prove that if A,B,C, are the angles of an arbitrary triangle, then
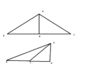
m(A)+m(B)+m(C) = 180 degrees by the following method: From any vertex draw the perpendicular to the line of the opposite side. Then use the result already known for right triangles
Homework Equations
The Attempt at a Solution
I think I can break this proof down into 3 cases
a right triangle, with base b and height h, with the perpendicular of the vertex
a triangle with height h, and a base b+x, x>0 where its perpendicular is x units to the left of the right triangles perpendicular
a triangle with height h, and a base b+k k<0 where its perpendicular is k units to the left of the right triangles perpendicular
am I right here or are there other cases i need to consider?
Last edited: