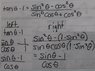Prove the trigonometric identity

[pbonnie]

Homework Statement

(question attached)

Homework Equations

The Attempt at a Solution

Checking solution.. pretty sure I did this wrong.
(solution attached)

 

[Mark44]

Homework Statement

(question attached)

Homework Equations

The Attempt at a Solution

Checking solution.. pretty sure I did this wrong.
(solution attached)

Yes, you did. I see several mistakes.

On the left side, tanθ - 1 = sinθ/cosθ - 1, but that's not equal to (sinθ - 1)/cosθ, as you show.

On the right side there are two mistakes that I see: you factored the denominator wrong in the next to the last line, and I have no idea how you ended with what you did in the last line.

 

[Mark44]

I would recommend working with the right side, to make it look like the left side. This can be done in three steps.

 

[pbonnie]

Oh wow okay, I think I got it. Thank you very much

 

[pbonnie]

Sorry nevermind, I see what you were saying earlier now. So the last step on the right side would be to simplify it further to tanθ -1

 

[Mark44]

Oh wow okay, I think I got it. Thank you very much

No, you're not getting it at all. On the right side, you have this:
$$ \frac{sin^2(θ) - cos^2(θ)}{sin(θ)cos(θ) + cos^2(θ)} = \frac{sin^2(θ) - 1}{sin(θ)cos(θ)}$$

This is wrong. It appears that you are cancelling the cos²(θ) terms to arrive at the expression on the right, above. This is like saying (5 + 1)/(2 - 1) = (5 - 1)/2 = 2. The actual value is 6.

The only time you can cancel is when the same factor (not term) appears in the numerator and denominator. You will not be successful in trig until you get a stronger grasp on algebra.

 

[pbonnie]

No matter what I do I can't get the answer. I don't understand.

 

[Mark44]

Do you know how to factor a² - b²?
Can you factor ab + b²?

You need to know how to make these factorizations so that you can simplify this:
$$ \frac{sin^2(θ) - cos^2(θ)}{sin(θ)cos(θ) + cos^2(θ)} $$

The way you did it is not valid.

 

[pbonnie]

So the numerator would be (sinƟ+cosƟ)(sinƟ+cosƟ)
But I don't know how to factor ab + b^2

 

[pbonnie]

Oh! ab + b^2 would equal b(a+b)?
So the denominator would be cosƟ(sinƟ + cosƟ)?

 

[Mark44]

No matter what I do I can't get the answer.

It's because you do not understand how to simplify fractions and rational expressions.

In post #1 you did this:

$$ \frac{sin^2(θ) - (1 - sin^2(θ))}{sin(θ) cos(θ) (1 - sin^2(θ))} ~~\text{(1)}$$
$$ \frac{sin^2(θ) - 1}{sin(θ) cos(θ)} ~~\text{(2)}$$
$$ \frac{sin(θ) - 1 }{cos(θ)} ~~\text{(3)}$$

In (1) you have the wrong sign in the denominator.
In (2), you apparently canceled (1 - sin²(θ)). You absolutely can't do this, since what you canceled is not a factor of both numerator and denominator.
In (3), you apparently canceled sin(θ), which is also invalid since sin(θ) is not a factor of the numerator.

In post #4 you did this:
$$ \frac{sin^2(θ) - cos^2(θ)}{sin(θ) cos(θ) + cos^2(θ)} ~~\text{(4)}$$
$$ \frac{sin^2(θ) - 1)}{sin(θ) cos(θ) } ~~\text{(5)}$$
$$ \frac{sin(θ) - 1}{cos(θ) } ~~\text{(6)}$$

In (4), you have the sign in the denominator correct this time.
In (5), you canceled cos²(θ), which is not valid for the reasons stated above.
In (6), you sin(θ), which is also not valid. sin(θ) is not a factor in the numerator.

 

[Mark44]

So the numerator would be (sinƟ+cosƟ)(sinƟ+cosƟ)

If you multiply this back out do you get sin²(θ) - cos²(θ)?

Oh! ab + b^2 would equal b(a+b)?
So the denominator would be cosƟ(sinƟ + cosƟ)?

Yes!

 

[pbonnie]

Okay so now I have (sinƟ+cosƟ)(sinƟ+cosƟ)/cosƟ(sinƟ + cosƟ)
So now I can actually cancel out (sinƟ + cosƟ) once on the top and once on the bottom, to get
sinƟ + cosƟ/cosƟ

From here I'm stuck again. I know the sinƟ/cosƟ would equal tan, but I'm not sure where the -1 comes from

 

[Mark44]

Okay so now I have (sinƟ+cosƟ)(sinƟ+cosƟ)/cosƟ(sinƟ + cosƟ)

Does (sinƟ+cosƟ)(sinƟ+cosƟ) multiply out to sin²Ɵ - cos²Ɵ?

So now I can actually cancel out (sinƟ + cosƟ) once on the top and once on the bottom, to get
sinƟ + cosƟ/cosƟ

From here I'm stuck again. I know the sinƟ/cosƟ would equal tan, but I'm not sure where the -1 comes from

 

[pbonnie]

Ah sorry I had the right answer in my head but I wrote it out wrong. Didn't even notice.
(sinƟ+cosƟ)(sinƟ-cosƟ)/cosƟ(sinƟ + cosƟ)

Then sinƟ-cosƟ/cosƟ
Now I'm stuck again. I'm doing different variations of substituting the quotient identity into the equation but I can't get the right order

 

[Mark44]

Ah sorry I had the right answer in my head but I wrote it out wrong. Didn't even notice.
(sinƟ+cosƟ)(sinƟ-cosƟ)/cosƟ(sinƟ + cosƟ)

So far, so good, but you need some more parentheses around the entire denominator, like so:
(sinƟ+cosƟ)(sinƟ-cosƟ)/(cosƟ(sinƟ + cosƟ))

Then sinƟ-cosƟ/cosƟ

Here you need some parentheses around the entire numerator, like so:

(sinƟ-cosƟ)/cosƟ

Now I'm stuck again.

(A + B)/C is the same as A/C + B/C, and (A - B)/C is the same as A/C - B/C.

I'm doing different variations of substituting the quotient identity into the equation but I can't get the right order

You're having a lot of difficulties working with fraction-type expressions. It would be a good idea for you to take some time reviewing how to simplify fractions and rational expressions. If you don't still have the textbook you studied from, there are a number of online sites that are helpful, such as http://khanacademy.org.

 

[pbonnie]

Got it! sinƟ/cosƟ - cosƟ/cosƟ
= tanƟ-1

Ahh thank you so much. I definitely need a refresher it's been a long time since I've taken a math course. Thank you for the link and for you patience and help!