Prove this relation between two numbers (Number theory)

[LCSphysicist]

Homework Statement

If (u,v) = 1, prove that (u+v,u-v) is either 1 or 2.
u and v are integers.

Relevant Equations

.

If (u,v) = 1, prove that (u+v,u-v) is either 1 or 2.
Where (,) means:

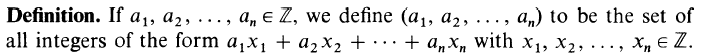
$$ux_1 + vx_2 = 1$$
$$u + v(x_2/x_1) = 1/x_1, u(x_1/x_2) + v = 1/x_2$$
$$u + v = 1/x_1 + 1/x_2 - v x_2/x_1 - u x_1/x_2$$
$$u - v = 1/x_1 - 1/x_2 + u x_1/x_2 - v x_2/x_1$$

Now we can express (u+v,u-v). But i am not sure if it will give us an answer.
I think the key is to know what x₁ and x₂ are, knowing that u and v are coprimes. But i don't know how to find it.

 

[BvU]

I am missing the
Homework Statement:
and
Relevant Equations:

For part of the first I can substitute " If (u,v) = 1, prove that (u+v,u-v) is either 1 or 2."
But one really needs a definition of (u,v).
And one needs to know what u and v are. Uruguaians, Venezolans ?

 

[LCSphysicist]

I am missing the
Homework Statement:
and
Relevant Equations:

For part of the first I can substitute " If (u,v) = 1, prove that (u+v,u-v) is either 1 or 2."
But one really needs a definition of (u,v).
And one needs to know what u and v are. Uruguaians, Venezolans ?

u and v are integer numbers hahaha
You are right, i forgot to write the meaning of (,).
I will edit

 

[Delta2]

I don't understand how that definition of (u,v) that is given in post #1 is equivalent to that u,v are co primes.

 

[LCSphysicist]

I don't understand how that definition of (u,v) that is given in post #1 is equivalent to that u,v are co primes.

(u,v) = 1
ux + vy = 1 (1)​

" Bézout's identity — Let a and b be integers with greatest common divisor d. Then there exist integers x and y such that ax + by = d. More generally, the integers of the form ax + by are exactly the multiples of d. "

if a and b are co primes, gcd = 1
ax + by = 1

As in our case (1)

 

[Delta2]

Sorry there is something i don't understand, let's take 5 and 2 that are coprimes, $5\times10+2\times25=100\neq 1$

Something that you don't explain well, you saying for every $x_1,x_2$ or do you mean there exist $x_1,x_2$ such that

 

[BvU]

u and v are integers. Interesting.

Then what does it mean if you write "(u,v)=1" ?
That the set of all integers of the form ux₁ + vx₂ consists of one and only one element, namely 1 ?

 

[Office_Shredder]

1 here represents the ideal generated by 1, or to put it a bit simply the set of all multiples of 1. This is equivalent to saying 1 is the smallest natural number that can be represented this was.

I think the solution to this is once you have a way of showing (u,v)=1, it's easy to give a representation that shows (u+v,u-v) contains 2, and hence is either 2 or 1.