Anzas
- 87
- 0
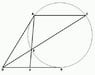
AD and BD touch the circule at points A and B
AC is parallel to BD
prove that:
1. DF^2 = AF*EF
2. BF = DF
its obvious that BF^2 = EF * AF i tried proving that DF = FB but with no luck.
edit: i uploaded the wrong picture earlier, terribly sorry i have so many of them
AC is parallel to BD
prove that:
1. DF^2 = AF*EF
2. BF = DF
its obvious that BF^2 = EF * AF i tried proving that DF = FB but with no luck.
edit: i uploaded the wrong picture earlier, terribly sorry i have so many of them
Attachments
Last edited: