Proving Quadrilateral PQRS is a Parallelogram

  • Thread starter Thread starter physics kiddy
  • Start date Start date
  • Tags Tags
    Geometry
Click For Summary

Homework Help Overview

The discussion revolves around proving that quadrilateral PQRS is a parallelogram based on the properties of angles formed by angle bisectors in the figure provided. The original poster attempts to establish a relationship involving angles QOP, R, and S.

Discussion Character

  • Exploratory, Assumption checking, Problem interpretation

Approaches and Questions Raised

  • Participants explore the relationship between angles in a pentagon and the implications for the quadrilateral's properties. There are attempts to express the sum of angles in terms of known variables and to derive relationships from triangle properties.

Discussion Status

Some participants have provided insights into the relationships between angles and have suggested methods to approach the problem. There is acknowledgment of multiple methods to reach a solution, but no consensus on a single approach has been reached.

Contextual Notes

Participants note the sum of angles in a pentagon and the relationships among angles in triangles, indicating that certain assumptions about angle measures are being examined. The original poster mentions finding a solution in a book, which adds a layer of complexity to the discussion.

physics kiddy
Messages
135
Reaction score
1
Recently, I bought a book and found a strange question :

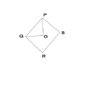
In the given figure, PQRS is a quadrilateral. PO and QO are bisectors of angle P and angle Q respectively, then prove that angle QOP = 1/2 (angle R + angle S)

I made several attempts to get the solution but failed. I guess, we need to prove that PQRS is a parallelogram.
 

Attachments

  • Question.jpg
    Question.jpg
    4.5 KB · Views: 438
Physics news on Phys.org
Write out the sum of angles of the yellow pentagon.

ehild
 

Attachments

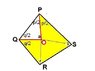
  • quadrilateral.JPG
    quadrilateral.JPG
    9.5 KB · Views: 494
It's 540 degrees.
 
physics kiddy said:
It's 540 degrees.

OK. How is the angle a related to p/2 and q/2? What is the sum of angles of the pentagon in terms of a, p/2, q/2, r and s?

ehild
 
Last edited:
In triangle QOP, determine angle QOP, hence determine reflex angle QOP.
 
Physics kiddy disappeared...

p/2+q/2=180-a (triangle)
p/2+q/2+r+s+360-a=540 (pentagon) -->

180-a+r+s+360-a=540, 2a=r+s.

ehild
 
Thank you ! Thank you again. I disappeared because I found the solution in a book. But you wrote a completely new and easy method to solve this question. Now, I have got two ways to solve this question.
 
I would like to see that solution from the book so much! Could you please show it?:smile:

ehild
 

Similar threads

Coordinate Geometry: PQRS Parallelogram
  • · Replies 1 ·
Replies
1
Views
2K
MHB Prove Geometry Challenge: Cyclic Quadrilateral PQRS
  • · Replies 2 ·
Replies
2
Views
2K
Proving Area of Parallelogram PQRS with Geometry Proof
  • · Replies 2 ·
Replies
2
Views
3K
Vector algebra (proving you have a parallelogram by using vectors)
  • · Replies 7 ·
Replies
7
Views
4K
Undergrad Vector Geometry: Proving Quadrilateral PQRS is a Parallelogram
  • · Replies 1 ·
Replies
1
Views
3K
Proving Perpendicular Lines in a Quadrilateral
  • · Replies 3 ·
Replies
3
Views
4K
High School Inscribed Quadrilateral Perpendicular Bisectors Convergence Theorem
  • · Replies 1 ·
Replies
1
Views
2K
Can the dot and cross product prove the sum of squares in a parallelogram?
  • · Replies 6 ·
Replies
6
Views
2K
Help with proving a quadrilateral is a parallelogram.
  • · Replies 5 ·
Replies
5
Views
5K
Proving the Bisectors of a Quadrilateral Bisect Each Other
  • · Replies 3 ·
Replies
3
Views
7K