Proving Rotation of Conic Using Polar Equations: Am I on the Right Track?

  • Thread starter Thread starter ballahboy
  • Start date Start date
  • Tags Tags
    Rotation
Click For Summary
SUMMARY

The discussion focuses on proving the rotation of conic sections using polar equations, specifically through the transformation of coordinates. The user correctly identifies the transformation equations x' = rcos(θ - α) and y' = rsin(θ - α) as foundational to the proof. They also apply the difference identities to express these in terms of θ and α. However, they express uncertainty about the next steps in the proof, particularly regarding the interpretation of rsin(α) and rcos(α).

PREREQUISITES
  • Understanding of polar coordinates and their relationship to Cartesian coordinates.
  • Familiarity with trigonometric identities, particularly the sine and cosine difference identities.
  • Basic knowledge of conic sections and their properties.
  • Experience with matrix transformations in coordinate geometry.
NEXT STEPS
  • Study the derivation of polar coordinate transformations in conic sections.
  • Learn about the application of trigonometric identities in coordinate transformations.
  • Explore matrix representations of transformations for conic sections.
  • Investigate the geometric interpretation of rotation in polar coordinates.
USEFUL FOR

Students of mathematics, particularly those studying geometry and conic sections, as well as educators seeking to enhance their teaching methods in coordinate transformations.

ballahboy
Messages
34
Reaction score
0
Ok. So i got that part where you replace x with x'cos(theta)+y'sin(theta) and y with -x'sin(theta)+y'cos(theta). My book shows us the proof for this using matrices. What my teacher wants us to do its prove this using polar equations or something like that.

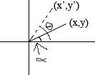
I started out with the drawing attached(teacher told us to use it). From that i got x'=rcos(theta-alpha) and y'=rsin(theta-alpha). Using the difference identities, i got x'=rcos(theta)cos(alpha)+rsin(theta)sin(alpha) and y'=rsin(theta)cos(alpha)-rcos(theta)sin(alpha). I kinda got stuck after this.. Am i on the right track at all? or is it completely off
 

Attachments

  • Untitled-1.jpg
    Untitled-1.jpg
    1.9 KB · Views: 414
Physics news on Phys.org
Line up the corresponding equations.

What is rsin(alpha)? and rcos(alpha)?
 
robphy said:
What is rsin(alpha)? and rcos(alpha)?

umm.. iono about that but I know that rsin(theta) is y and rcos(theta) is x.. would that be the same?
 

Similar threads

Deriving ODEs for straight lines in polar coordinates for a given Lagrangian
  • · Replies 8 ·
Replies
8
Views
2K
What Is the Electric Field of a Curved Rod at the Origin?
  • · Replies 9 ·
Replies
9
Views
4K
Tension developed in a charged ring
  • · Replies 2 ·
Replies
2
Views
2K
How Do You Calculate the Electric Potential of a Square Plate?
  • · Replies 6 ·
Replies
6
Views
2K
How can I find the velocity of a point on a disk rotating in a disc?
  • · Replies 16 ·
Replies
16
Views
2K
Undergrad Coordinate transformation for isotropy
  • · Replies 7 ·
Replies
7
Views
1K
Work done on a conical pendulum
  • · Replies 3 ·
Replies
3
Views
2K
Elliptical motion in polar coordinates
  • · Replies 10 ·
Replies
10
Views
1K
MIT OCW, 8.02 Electromagnetism: Potential for an Electric Dipole
  • · Replies 1 ·
Replies
1
Views
3K
Morin 3.7 -- Block sliding sideways on an inclined plane
  • · Replies 11 ·
Replies
11
Views
1K