Cantor
- 8
- 0
I have a question involving the measure of segments
If m is a point inside a triangle ABC how could we prove that segment BM+CM < AB+AC. I am trying to use the Triangle Inequality Theorem (If A, B, C are three non-collinear points then AC < AB+BC) but I am stuck.
Should I prove by contradiction or show that BM < AB and CM <AC
Any help would be appreciated, Thanks
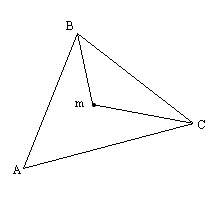
If m is a point inside a triangle ABC how could we prove that segment BM+CM < AB+AC. I am trying to use the Triangle Inequality Theorem (If A, B, C are three non-collinear points then AC < AB+BC) but I am stuck.
Should I prove by contradiction or show that BM < AB and CM <AC
Any help would be appreciated, Thanks