estudent1371
- 5
- 1
- Homework Statement
- Using R1, R2, ℰ and C along with Kirchhoff’s laws, prove the formulas in equations (7) and (8).
- Relevant Equations
- time constant charging
(7) t_c=(R_1 R_2)/(R_1+R_2 ) C
time constant discharging
(8) t_d=R_2 C
the attached files are a diagram of the circuit. also I believe I figured out how to proof equation (7) but I'm lost on how to proof (8)
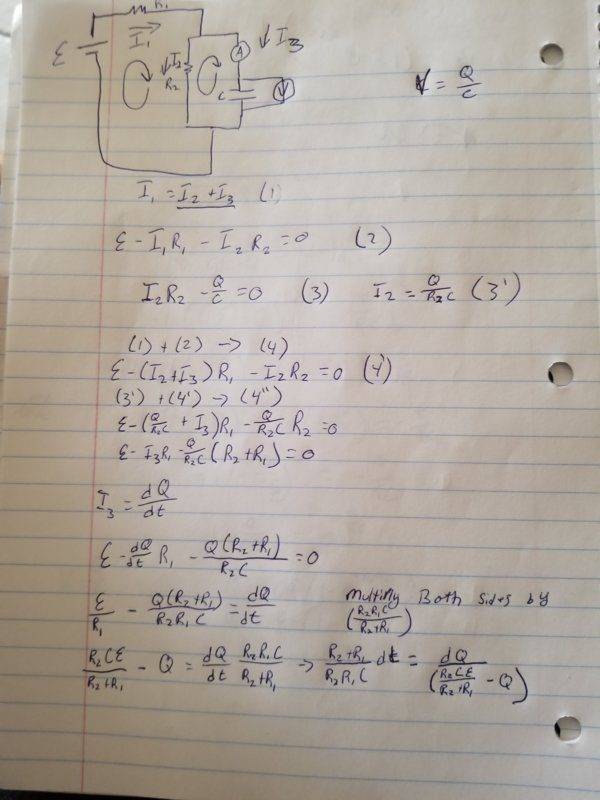

 How can you justify that?
How can you justify that?