inv4lid
- 19
- 0
Homework Statement
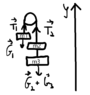
Determine bodies' acceleration if their masses are the following: m1 = 25kg, m2 = 1kg, m3 = 3kg and the Tension of the ropes. Friction is neglected, as well as the mass of the pulley. It is considered that the ropes are perfect.
m1 = 25kg;
m2=1kg;
m3=3kg;
___________
a=?
T1=?
T2=?
#
Homework Equations
For the first object we have:
T1-G1= m1*a; (the acceleration is oriented upwards)
a = (T1-G1)/m1;
For next ones, I guess:
The acceleration here goes downwards
T2-G2-G3 = -(m2+m3)*a;
a = (T2-G2 - G3) / -(m2 + m3)
Are the accelerations the same?
How would i find it?