Pulley system with a weight's acceleration of g/5

[DocZaius]

Homework Statement

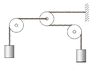
In the system shown in the figure (see attachment), the pulleys on the left and right are fixed, but the pulley in the center can move to the left or right. The two masses are identical. Show that the mass on the left will have an upward acceleration equal to g/5. Assume all the ropes and pulleys are massless and frictionless.

Homework Equations

F=ma

The Attempt at a Solution

I will call the left rope's tension T1 and the right rope's tension T2. The left weight will be called "a" and the right weight will be called "b".

Net force on a = T1 - mg
Net force on b = T2 - mg

acceleration of a = T1/m - g
acceleration of b = T2/m - g

Forces on middle pulley = T2*2 - T1

I have approached this problem from many angles and I just can't come up with an equation that uses both tensions because the middle pulley being massless makes it impossible to find an acceleration for it.

Since F=ma, when mass is 1/infinity, acceleration becomes infinity. So I can't find the acceleration of the middle pulley that way.

Furthermore, despite every other approach I've used, I just can't get "g/5" for the left weight's acceleration.

 

[Doc Al]

You are missing:
(1) The relationship between T1 and T2. (Analyze forces on the moving pulley. What must the net force equal?)
(2) The relationship between the acceleration of each mass due to the fact that they are interconnected. (Figure out this constraint.)

 

[DocZaius]

You are missing:
(1) The relationship between T1 and T2. (Analyze forces on the moving pulley. What must the net force equal?)

net force on middle pulley=T2*2 - T1 is what I listed as the relationship between the tensions. I can't think of another relationship to list. I don't know what the net force must equal. I know that the middle pulley's acceleration must equal g/5 but I have two things to say about that. First knowing the acceleration of the pulley doesn't tell me the ultimate net force on the pulley since to figure it out, the pulley would need to have a mass that is not negligible. Secondly, I do not want to solve this problem using g/5 as a starting point. I want to figure out how he got g/5 in the first place.

(2) The relationship between the acceleration of each mass due to the fact that they are interconnected. (Figure out this constraint.)

I do not know the relationship between the two masses' accelerations. Since the tension of one rope depends on the tension of the other, I first need to link them in another way than T2*2 - T1. I can't think of that other way.

 

[Doc Al]

net force on middle pulley=T2*2 - T1 is what I listed as the relationship between the tensions. I can't think of another relationship to list. I don't know what the net force must equal.

Sure you do. What's the mass of the pulley? Apply Newton's 2nd law.

I do not know the relationship between the two masses' accelerations.

There's a simple kinematic relationship between the two masses. When mass "a" moves up 1 meter, how far does mass "b" move down? (There are several ways to figure this out. One good way is just to play around with a piece of string.)

 

[DocZaius]

Sure you do. What's the mass of the pulley? Apply Newton's 2nd law.

The mass is negligible, so I will say it is 1/(infinity)

F=ma
when m = 1/(infinity), the equation stops being useful.

There's a simple kinematic relationship between the two masses. When mass "a" moves up 1 meter, how far does mass "b" move down? (There are several ways to figure this out. One good way is just to play around with a piece of string.)

I think b moves down 1/2 meter, but I will think about it more.

 

[Doc Al]

The mass is negligible, so I will say it is 1/(infinity)

F=ma
when m = 1/(infinity), the equation stops being useful.

Treat the pulley as massless, so m = 0. Just plug that into the equation. (Not useless at all.)

I think b moves down 1/2 meter, but I will think about it more.

That's incorrect, but you're on the right track. Think about it some more.

 

[DocZaius]

Got g/5! Thanks Doc Al!