Pulleys and Gravity: Solving Acceleration for m1 & m2

[ace214]

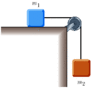
In Figure P4.30, m1 = 9.5 kg and m2 = 3.5 kg. The coefficient of static friction between m1 and the horizontal surface is 0.60 while the coefficient of kinetic friction is 0.30.

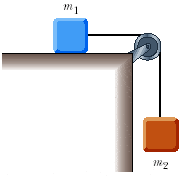(Why can't I post this image in the message?)
In case you don't feel like looking at the picture, there are two masses connected by a frictionless pulley- m1 is on the table, m2 is hanging off the table.

(a) If the system is released from rest, what will its acceleration be?
(b) If the system is set in motion with m2 moving downward, what will be the acceleration of the system?

=========================================

I assume that the basic equation is the same for both parts just with different coefficients of friction. (Is this correct?) So I start with

m1a1 = T - forceFriction
m2a1 = T - m2g

Then I plug in -a1 for a2 in the second problem giving me -m2a1 = T - m2g => m2a1 = -T +m2g

Then add these two equations together, canceling out the tension.

m1a1 + m2a1 = m2g - Ff => a1(m1 + m2) = m2g - Ff


Then I solve for a using +9.8 for g in all cases. I eventually get -1.66 but this is not the answer. WebAssign says it differs by order of magnitude...

==========================================

I think something may be wrong with my signs in one way or another but I have tried multiple ways. Thanks for any help.

 

[TVP45]

Are you combining the two questions? You should treat them separately. The equations will be the same except that the frictional force will be different.

 

[ace214]

Yes, that's what I said. No, I have just tried one (using the static friction) to see if I've got it right, because feedback is given immediately. I didn't want to use up all my chances in both.

Any help as to the answer?

 

[Doc Al]

static case

Realize that static friction can have any value up to the maximum of \mu N; you can't just say that it equals that maximum value. The first thing you have to answer is: Can the hanging mass exert enough force to overcome the static friction?

 

[stewartcs]

Have you considered for case (a) that the block would not accelerate (i.e. zero acceleration)?

Hint: Does m2 generate enough force to overcome the static friction force of m1?

 

[ace214]

Ahhh.. Ok. But shouldn't the equations have worked anyway and just gotten 0?
Also, I got it to work for kinetic friction.

 

[Doc Al]

But shouldn't the equations have worked anyway and just gotten 0?

No, because your equation had friction = \mu N, which isn't true for static friction. (Static friction is less than or equal to that maximum value, as needed.)

Also, I got it to work for kinetic friction.

Sure, since kinetic friction does equal \mu N.

 

[ace214]

So is there a way to plug it into such an equation or will it always be "is this force greater than friction?"

 

[Doc Al]

The fact that you got a negative acceleration should have been a tip-off. You should know that the only way this thing could accelerate is in the + direction (to the right and down).

But there's no substitute for reasoning it out.

 

[ace214]

Ok, thanks a lot.