What are the weights A and B in this system?

[alephnull]

Homework Statement

For some reason, this question's really stumped me. The text reads:
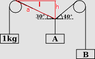
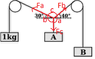
"The system shown is in static equilibrium. Use the principle of virtual work to find the weights A and B. Neglect the weight of the strings and the friction in the pulleys."
And has the accompanying diagram:
http://img143.imageshack.us/img143/9292/path2405.png
EDIT: oops; that 40° should read 45°; sorry about that.

For variables, I think we have:
A and B (obviously)
Perhaps rope tension?

Homework Equations

Not sure, to be honest.

The Attempt at a Solution

Based on what I've looked at previously with the principle of virtual work, I'd say I would have to generate a pair of equations based on the imagined movement of the weights and then solve the two simultaneously to get the values for A and B, but it's here it all falls down: I can't figure out how far the 1kg weight would rise if weight A fell, say, 2 metres. Of course, this method could be fundamentally flawed anyway and it wouldn't really matter.

(Yes, this is the second exercise from the exercise section of Feynman's Tips on Physics; having picked up the Feynman Lectures to try and learn some more advanced physics on my own than what is being taught in my school, there are more than a few gaps in my knowledge which lead to situations such as this where the question seems only tangentially related the the actual lecture)

 

[dr.fizix]

As for the distances that the weights would move, you should assume that the distances you pull on the weights are extremely small. It may be best to move the middle weight, A, down a distance δ. If the distance pulled is very small, the weight should not move left or right, just down. Then you will have to use Pythagorean's theorem to figure out the change in lengths of the string from wieght A to either of the pulleys.

That's what I have come up with so far - and it gives you ONE equation to work with. The other equation, though, I'm not sure about yet - perhaps it could be if you move the wieght A a distance δ in the opposite direction (?).

 

[2milehi]

Can't the sum of forces in the x and y direction help you out?

 

[cupid.callin]

Based on what I've looked at previously with the principle of virtual work, I'd say I would have to generate a pair of equations based on the imagined movement of the weights and then solve the two simultaneously to get the values for A and B, but it's here it all falls down: I can't figure out how far the 1kg weight would rise if weight A fell, say, 2 metres. Of course, this method could be fundamentally flawed anyway and it wouldn't really matter.

Hi alephnull
Welcome to PF !

For your distance part ...

Consider the red triangle ... And use Pythagoras

a^2 = l^2 + h^2

Now if A moves down by 1 meter ... new h is h+1 ... l is same ...

a'^2 = l^2 + (h+1)^2

Now use there equations ...

BTW, why are you finding this ?

 

[2milehi]

That does not seem like the right approach. There is no guarantee that the weight will go stright down - the weight could shift left/right.

 

[cupid.callin]

That does not seem like the right approach. There is no guarantee that the weight will go stright down - the weight could shift left/right.

I was just answering OP's question ... And the block won't go anywhere ... the question says that its in static equilibrium

 

[2milehi]

I was just answering OP's question ... And the block won't go anywhere ... the question says that its in static equilibrium

Then why state the equations with regards to A being pulled down one meter?

 

[cupid.callin]

Then why state the equations with regards to A being pulled down one meter?

As i said before, Because the OP asked how to find it ...
And if you look up you'll find this:

BTW, why are you finding this ?

That satisfies you ?

 

[2milehi]

As i said before, Because the OP asked how to find it ...
And if you look up you'll find this:
That satisfies you ?

And if the OP asks if crossing a busy highway is a good choice and you say to look both ways before crossing I would question your advice. The OP is going down the wrong road and you are helping him out. When giving advice one should give it to the best of their ability and one might have to steer the person asking the question.

 

[cupid.callin]

And if the OP asks if crossing a busy highway is a good choice and you say to look both ways before crossing I would question your advice. The OP is going down the wrong road and you are helping him out. When giving advice one should give it to the best of their ability and one might have to steer the person asking the question.

Cut it out, will ya? Why, for most of people on the website, winning an argument so important?
It was my mistake, happy now?




(But OP will still learn something from crossing the road)

 

[2milehi]

Unless the OP gets hit by a car and dies and learns nothing. This is an open discussion where ideas are exchanged. I am not out to win an argument, but if something doesn't seem right, I will say so.

 

[NascentOxygen]

Homework Statement

Does your book supply the answers? It would help if you gave the answers, along with the question, when known.

 

[heartOFphysic]

HELLO

this questions interests me.

Could you possibly go along this route.

Let the 1Kg mass= W1, A= W2 and B=W3

then Let the tension in String 1 = F1 string 2= F2 and string3 =F3 (see THE IMAGE HERE OTHERWISE THE FOLLOWING WON'T MAKE SENSE)

and so will F1=W1 F2 = W3 and F3=W2

Since you already know what W1 is (1kg= 9.8N) so you know F1. then you are given angles, so can you resolve vectors to give you vertical and horizontal components of each string, thus you'll have everything, and so you can find A and B.

See image (makes things clearer)

 

[heartOFphysic]

am I right guys? anyone?

 

[cupid.callin]

and so will F1=W1g F2 = W3g and F3=W2g

heartOFphysic method is good ...

Perhaps we can also use a very simple theorem here,
I don't remember the name but it goes something like this ...

\Large{\frac{F_a}{sin a} = \frac{F_b}{sin b} = \frac{F_c}{sin c}}

This might prove to be a bit lengthy here but its always good to know an extra method ...

 

[NascentOxygen]

this questions interests me.

Could you possibly go along this route.

Let the 1Kg mass= W1, A= W2 and B=W3

then Let the tension in String 1 = F1 string 2= F2 and string3 =F3 (see THE IMAGE HERE OTHERWISE THE FOLLOWING WON'T MAKE SENSE)

and so will F1=W1 F2 = W3 and F3=W2

Since you already know what W1 is (1kg= 9.8N) so you know F1. then you are given angles, so can you resolve vectors to give you vertical and horizontal components of each string, thus you'll have everything, and so you can find A and B.

There is nothing to prevent you using this method, but you should not anticipate getting any marks for doing so. The question states specifically the method to be used, and all students know that you ignore instructions to your peril. Resolution of forces is a good method for checking your answer, but is not suitable as your answer. Let me quote the instructions:

The text reads:
"The system shown is in static equilibrium. Use the principle of virtual work to find the weights A and B. Neglect the weight of the strings and the friction in the pulleys."