derekbeau
- 17
- 0
http://s1.lite.msu.edu/res/msu/stump/Energy101/pumpedstorage.gif
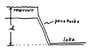
Consider the Ludington Pumped Storage Plant. Water may flow out of the reservoir, through the penstocks, and down into Lake Michigan, at a volume rate of 1710 m3/s. The water is directed through turbines to turn electric generators to make electric power. The height of the water in the reservoir is h = 100 meters above the surface of Lake Michigan. How much power ( = energy per unit time) would be available if the Plant is operating with these parameters?
Tip: In one second the height of the surface drops by Deltah where ρ×A×∆k=μ×(1 sec). (ρ is the density of water, 1.0×103 kg/m3.) How much has the gravitational potential energy changed?
Ok So what i have done so far is convert the volum to mass
1710 m^3/s * 1000 kg/m^3 = 1710000 kg/s
Then I thought id use the formula
P = Mgh
P = 1710000 * 9.81 * 100
and I got 1677510000 (watts?)
Well that wasnt the right answer, so i tried converting to kilowatt-hours
1677510000 W / 3600000 J = 465.975 kWh
Still not right.
I think my problem is because either the height of the water is changing, or i am using an incorrect height. I don't know. But any help would be great. (it is due tomorrow)
Thanks
Consider the Ludington Pumped Storage Plant. Water may flow out of the reservoir, through the penstocks, and down into Lake Michigan, at a volume rate of 1710 m3/s. The water is directed through turbines to turn electric generators to make electric power. The height of the water in the reservoir is h = 100 meters above the surface of Lake Michigan. How much power ( = energy per unit time) would be available if the Plant is operating with these parameters?
Tip: In one second the height of the surface drops by Deltah where ρ×A×∆k=μ×(1 sec). (ρ is the density of water, 1.0×103 kg/m3.) How much has the gravitational potential energy changed?
Ok So what i have done so far is convert the volum to mass
1710 m^3/s * 1000 kg/m^3 = 1710000 kg/s
Then I thought id use the formula
P = Mgh
P = 1710000 * 9.81 * 100
and I got 1677510000 (watts?)
Well that wasnt the right answer, so i tried converting to kilowatt-hours
1677510000 W / 3600000 J = 465.975 kWh
Still not right.
I think my problem is because either the height of the water is changing, or i am using an incorrect height. I don't know. But any help would be great. (it is due tomorrow)
Thanks
Last edited by a moderator: