WeiShan Ng
- 36
- 2
Homework Statement
Hi, I was reading Griffiths and stumble upon some questions. This is from 5.1.2 Exchange Forces. The section is trying to work out the square of the separation distance between two particles, $$\langle (x_1 - x_2)^2 \rangle = \langle x_1^2 \rangle + \langle x_2^2 \rangle - 2 \langle x_1 x_2 \rangle$$
My confusion came when
$$\int x_1 \psi_a (x_1)^* \psi_b (x_1) dx_1 \, \int x_2 \psi_b(x_2)^* \psi_a(x_2) dx_2 = \langle x \rangle _{ab} \langle x \rangle _{ba}$$ I don't get why there are ##\langle x \rangle _{ab}## and ##\langle x \rangle _{ba}## here , won't the $$\int x_2 \psi_b(x_2)^* \psi_a(x_2) dx_2=\int x_1 \psi_a (x_1)^* \psi_b (x_1) dx_1=0??$$ since both ##\psi_a## and ##\psi_b## are orthogonal to each other?
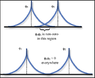
And in the next paragraph the text says
What is the meaning of "overlap" here? Based on the text given I assume it means both particles are "at the same position", i.e. ##x_1=x_2##. And how does an overlapping and non-overlapping wavefunction look like?Notice that ##\langle x \rangle _{ab} ## vanishes unless the two wavefunctions actually overlap [if ##\psi_a(x)## is zero wherever ##\psi_b(x)## is nonzero, the integral in Equation 5.20 is zero] So if ##\psi_a## represents an electron in an atom in Chicago, and ##\psi_b## represents an electron in an atom in Seattle, it's not going to make any difference whether you antisymmetrize the wave function or not. As a practical matter, therefore, it's okay to pretend that electrons with nonoverlapping wave functions are distinguishable.