maxverywell
- 197
- 2
What are the coordinates on the 3D Bloch ball of a qubit's mixed state of the form:
##\rho=p_{00}|0\rangle \langle 0|+p_{01}|0\rangle \langle 1|+p_{10}|1\rangle \langle 0|+p_{11}|1\rangle \langle 1|##
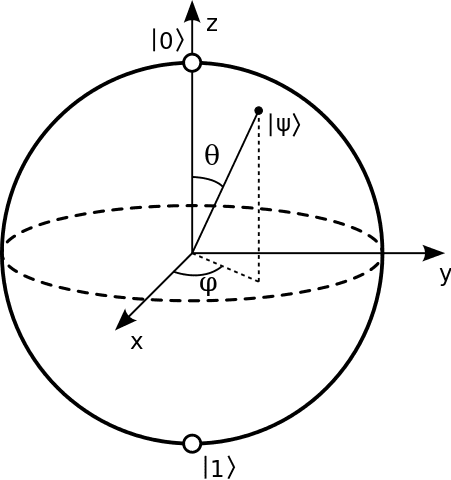
##\rho=p_{00}|0\rangle \langle 0|+p_{01}|0\rangle \langle 1|+p_{10}|1\rangle \langle 0|+p_{11}|1\rangle \langle 1|##
Last edited: