- #1
chrisych
- 32
- 0
Does anyone know how to calculate these questions?
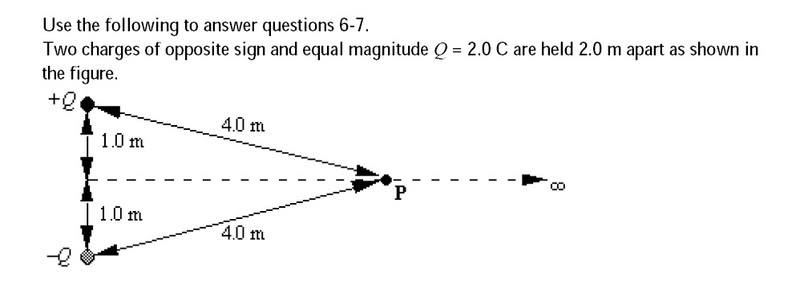

Doc Al said:Do your own work, show what you did and where you got stuck, and then you'll get plenty of help.
Doc Al said:You are dealing with point charges here: Look up expressions for the electric field and electric potential at a given distance from a point charge. Note that electric field is a vector, but potential is a scalar.
Electric field is a vector, so direction counts. Add them like vectors.chrisych said:E = Q / (4 pi eo r^2)
For +Q, E1 = Q / (4 pi eo 4^2) = Q / (64 pi eo)
For -Q, E2 = -Q / (4 pi eo 4^2) = -Q / (64 pi eo)
E1 + E2 = ?
Good!V = Q / (4 pi eo r)
For +Q, V1 = Q / (4 pi eo 4) = Q / (16 pi eo)
For -Q, V2 = -Q / (4 pi eo 4) = -Q / (16 pi eo)
V1 + V2 = 0 and so this is the correct answer?
That would be true if E1 and E2 were perpendicular, but they are not. Consider the horizontal & vertical components of each.chrisych said:|E| = sqrt (E1^2 + E2^2)
Doc Al said:That would be true if E1 and E2 were perpendicular, but they are not. Consider the horizontal & vertical components of each.
Typo here; this should be:chrisych said:|E| = |Horizontal Component of E| + |Vertical Component of E|
Doc Al said:You got it!
Typo here; this should be:
|E|^2 = |Horizontal Component of E|^2 + |Vertical Component of E|^2
Charge is a fundamental property of matter that describes its ability to interact with electromagnetic fields.
The two types of charge are positive and negative. Positive charge is associated with protons, and negative charge is associated with electrons.
Charge is measured in units of coulombs (C) using a device called an electrometer.
No, according to the law of conservation of charge, charge cannot be created or destroyed, only transferred from one object to another.
Charge creates electric fields, and electric fields can exert forces on other charges. The strength of the electric field is directly proportional to the amount of charge present.