chrisych
- 32
- 0
Does anyone know how to calculate these questions?

Doc Al said:Do your own work, show what you did and where you got stuck, and then you'll get plenty of help.
Doc Al said:You are dealing with point charges here: Look up expressions for the electric field and electric potential at a given distance from a point charge. Note that electric field is a vector, but potential is a scalar.
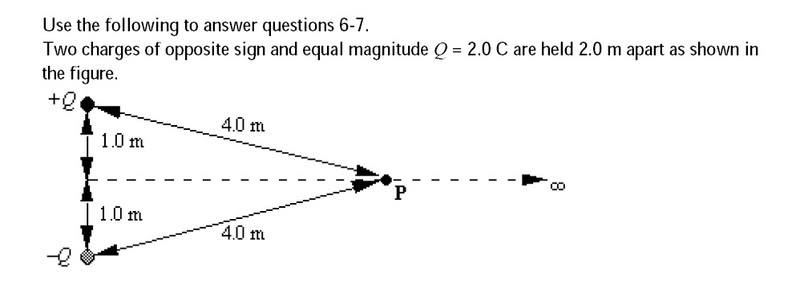
Electric field is a vector, so direction counts. Add them like vectors.chrisych said:E = Q / (4 pi eo r^2)
For +Q, E1 = Q / (4 pi eo 4^2) = Q / (64 pi eo)
For -Q, E2 = -Q / (4 pi eo 4^2) = -Q / (64 pi eo)
E1 + E2 = ?
Good!V = Q / (4 pi eo r)
For +Q, V1 = Q / (4 pi eo 4) = Q / (16 pi eo)
For -Q, V2 = -Q / (4 pi eo 4) = -Q / (16 pi eo)
V1 + V2 = 0 and so this is the correct answer?
That would be true if E1 and E2 were perpendicular, but they are not. Consider the horizontal & vertical components of each.chrisych said:|E| = sqrt (E1^2 + E2^2)
Doc Al said:That would be true if E1 and E2 were perpendicular, but they are not. Consider the horizontal & vertical components of each.
Typo here; this should be:chrisych said:|E| = |Horizontal Component of E| + |Vertical Component of E|
Doc Al said:You got it!
Typo here; this should be:
|E|^2 = |Horizontal Component of E|^2 + |Vertical Component of E|^2