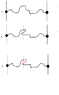
I'm not sure if it's the same idea as Feynman's, but I like the following sequence of pictures to show how something like negative probabilities can come into play.

Suppose that you have a string loosely hung between two points. I'm ignoring gravity, so the string has no tendency to droop down. We can possibly model the shape of the string as a random process giving the vertical position ##y## as a function of the horizontal position ##x##, as shown in Figure A above. The shape of the string is almost arbitrary, except for the fact that the ends are fixed and the function ##y(x)## must be continuous. (We might also want to constrain the length of the string, and maybe make the string a little stiff so that ##\frac{dy}{dx}## tends to be small, but that's unnecessary details for what I'm going to say.) We could describe the possibilities for the shape of the string by giving a function ##P(y,x)##, which is the probability that at horizontal position ##x## the vertical position of the string is ##y##. If the shape of string is sufficiently close to being straight, as in Figure A, then there will be only one value of ##y## for each value of ##x##, so we would demand that ##\int P(y,x) dy = 1##. For each ##x##, there is a probability of 1 that the string is at some vertical value ##y##.
Now, Figure B shows a less well-behaved shape of the string. The string is allowed to double-back on itself. So it's no longer true that for each ##x## there is exactly one value of ##y## to find the string. As shown in the figure, there are points, such as the location of the light vertical line, where there are 3 values of ##y## where the string can be located, for the same value of ##x##. So if we're trying to describe the string's shape using probabilities, we can no longer use a probability ##P(y,x)## that has to obey ##\int P(y,x) dy = 1## for each value of ##x##.
Probably the most elegant approach would be to treat ##x## and ##y## symmetrically, and consider them both random variables as a function of a path variable, ##s##. But for the purposes of motivating "negative probabilities", we can take the approach shown in Figure C. Rather than having a positive probability of finding the string at height ##y##, we introduce a counting function ##C(y,x)## that can be positive (to indicate the presence of a section of the string with ##\frac{dx}{ds} > 0##, where ##x## is the horizontal location, increasing to the right, and ##s## is the path parameter, which increases monotonically along the string) or negative (to indicate ##\frac{dx}{ds} < 0##, so it's a section of a string that has doubled back). In the figure, at the light vertical line, there are two positive sections of the string and one negative section. So counting orientation, it adds up to 1 string. So our constraint on the probabilistic function ##C(x,y)## would be that for each value of ##x##, ##\int C(x,y) dy = 1##, allowing both positive and negative values for ##C##.
If you think of the ##x## axis as being time, rather than a spatial dimension, then the string represents a worldline of a particle. The points where the string doubles back can be interpreted as particle/antiparticle pair creation, making three particles temporarily, two of which then annihilate each other.