Question about the delayed choice quantum eraser experiment

[al onestone]

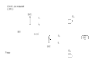
In the delayed choice quantum eraser experiment of 2000 (DCQE http://en.wikipedia.org/wiki/Delayed_choice_quantum_eraser) which I have attached a simplified figure for, there is the use of a downconversion crystal which converts pump photons into two photons of half the energy, signal and idler. In the DCQE, the pump is fed through one of two slits which are separated by 0.7mm, so there is the possibility that each photon may have traveled through either slit prior to downconversion. Since the two possible downconversion processes take place within the same crystal, they are coherent. Therefore there is the possibility of interference between the two downconversions.
The signal photons are fed to a detector where there may be interference observed. The interference there depends upon the "delayed choice" of the experimenter. Some of the idlers are reflected off the beamsplitters and detected, which implies "which path" information and negates the interference at the signal detector. Some idlers transmit through the beamsplitters and are forced to interfere with the other "possible path", which erases the which-path information. This allows interference at the signal detector, and it is noted by setting up coincidence counters between all detectors and post-selecting the idlers that transmitted.
Simple, and very similar to Mandel's ZWM from 1991 (but you'll notice the authors did not reference the ZWM). However, Mandel finds interference in the setup he uses without post-selection required. Why does the DCQE protocol require post-selection?

 

[Cthugha]

Simple, and very similar to Mandel's ZWM from 1991 (but you'll notice the authors did not reference the ZWM). However, Mandel finds interference in the setup he uses without post-selection required. Why does the DCQE protocol require post-selection?

The interference Mandel et al. see is single-photon interference. You would also see the pattern if Detector D_i was absent. A good discussion can be found in the quantum optics book written by Marlan O. Scully and Zubairy. In my edition it is on page 604. In a nutshell the setup used by Mandel et al. is somewhat similar to a Mach-Zehnder interferometer with added PDC crystals. In some sense you have some preselection here instead of postselection as only a very small portion of the emission from the PDC crystals will actually reach the detector and you need to align the setup such that you get indistinguishable photons for your chosen detector position.

In DCQE you typically deal with two-photon interference which always requires coincidence counting which in turn typically amounts to postselection.

 

[al onestone]

Sorry something happened to the figures when they converted.
To cthugha: Your comment "In DCQE you typically deal with two-photon interference which always requires coincidence counting which in turn typically amounts to postselection." tells me that you think Mandel is not using coincidence counting, which he is. The ZWM study is similar to the DCQE except without the delay, and without the choice, and no post-selection. But you're right about this "The interference Mandel et al. see is single-photon interference". And that differs drastically from the DCQE, because it uses coincidence interference between the transmitted idlers and the signal. I didn't notice this until I read your comment. On wikipedia and other sources they tend to lead you to believe that the interference is second order in the DCQE also, which it isn't. Thanks. Now I know this setup is useless for what I'm trying to do.

 

[Cthugha]

Sorry something happened to the figures when they converted.
To cthugha: Your comment "In DCQE you typically deal with two-photon interference which always requires coincidence counting which in turn typically amounts to postselection." tells me that you think Mandel is not using coincidence counting, which he is.

Sorry if my post was misleading. Mandel is using coincidence counting, but strictly speaking it would not be necessary under the conditions he was using. But of course in the present of stray light and a significant dark count rate it makes things much, much easier.

On wikipedia and other sources they tend to lead you to believe that the interference is second order in the DCQE also, which it isn't. Thanks. Now I know this setup is useless for what I'm trying to do.

I am not quite sure I get your point. In a typical DCQE experiment the interference is second order (in intensity), while it is first-order in Mandel's experiment. Or are you talking about fields? Then you indeed have second-order in Mandel's experiment and fourth-order in DCQE.

 

[al onestone]

Your question "Or are you talking about fields? Then you indeed have second-order in Mandel's experiment and fourth-order in DCQE." Yes, I'm talking about the order of the interference (the order of the correlation function in the quantization of the EM field). In typical experimental formalism one uses "2nd order" for a typical indistinguishability effect, and one would use "4th order" to describe a coincidence effect. In the theoretical formalism it is different however, in Ballentine and Glauber they use "1st order" and "2nd order" in their place.

To describre what I'm trying to do I am going to start a new thread. It will be about a modified DCQE which is suppose to produce 2nd order interference.

 

[Cthugha]

In typical experimental formalism one uses "2nd order" for a typical indistinguishability effect, and one would use "4th order" to describe a coincidence effect. In the theoretical formalism it is different however, in Ballentine and Glauber they use "1st order" and "2nd order" in their place.

Funny. I always perceived the usage of the wording the other way round. Theoreticians often tend to call the same thing second order and fourth order, while in most experimental papers I have read and written "standard" interference is termed first-order and intensity correlations are called second or even higher-order.

I assume it is rather a question of convenience and the school or quantum optics book one follows.