Question involving waves and a spring, help please?

[jcfor3ver]

Homework Statement

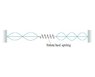
The two strings in the figure are of equal length and are being driven at equal frequencies. The linear density of the left string is 2.4 g/m

Homework Equations

AND ATTEMPT AT SOLUTION
Assume that while the spring provides the same tension to both strings it also acts as a fixed
point for the end of each string so an integral number of half wavelengths fit in each string.
Visualize: Use a subscript L for the left string and R for the right string. We are given μL = 2.0 g/m. From the
assumption above we know (Ts left ) = (Ts right ) = Ts . We are also given frequency left = frequ. right = frequency Notice from the
diagram that λleft=L and λright=2/3L
From v =λ f and s v = T /μ eliminate v and solve for μ : μ = T/(λ/f)^2

I am stuck here and keep getting the wrong answer. Can someone please explicitly solve this for me (include even algebraic steps because I keep just getting 2/3 for my answer)

 

[Nate810]

The Attempt at a SolutionSince the linear density of the left string is 2.4 g/m and the tension on both strings is the same, we can use the equation μ = T/(λ/f)^2 to find the linear density of the right string. We know that the tension on both strings is the same (Ts left ) = (Ts right ) = Ts and the frequency of both strings is the same (frequency left = frequ. right = frequency). Furthermore, since an integral number of half wavelengths fit in each string, we know that λleft=L and λright=2/3L. Therefore, we can plug in all of this information into the equation and solve for μ: μ = T/(λ/f)^2 = T/(2/3L/frequency)^2 = Ts^2/(4L^2/9f^2) = 9Ts^2/(4L^2f^2) Therefore, the linear density of the right string is equal to 9Ts^2/(4L^2f^2).