Question on equation for instantaneous E field along the transmission medium.

[yungman]

I am studying Poynting vectors. I run into question that I don't see any good explanation in all the books I have. All the books claimed
E_{(z,t)} =E_{(z=0)} Re[e_{j(wt-\beta z)} + \Gamma e_{j(wt+\beta z)}]

But sinse E0 is complex so this is what I have and is not equal to what the book gives. In fact the Electromagnetic by Ulaby actually say ignor the phase angle of E0! Below is what I have:

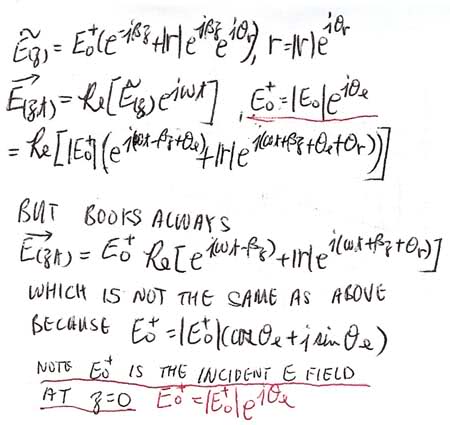
Obviously the answer does not agree. This is particularly obvious when working on Poynting vectors. Please tell me what do I miss in this whole thing.

Thanks

 

[ravioli]

Once you go into phasor domain, all information is just relative time. Therefore you can assume your Incident Phase Angle is zero. As well as that I believe that your book is assuming that maximum amplitude occurs at z=0(From your Latex Code). These two assumptions seem to be apparent in line 1, but not in line 3 of your derivations.

 

[yungman]

Once you go into phasor domain, all information is just relative time. Therefore you can assume your Incident Phase Angle is zero. As well as that I believe that your book is assuming that maximum amplitude occurs at z=0(From your Latex Code). These two assumptions seem to be apparent in line 1, but not in line 3 of your derivations.

But the book of Ulaby even expressly said that the incident E field at z=0 is complex and it has an angle. It just said they are going to ignor it! Ulaby simply say don't look at the phase angle of the incident E field and Cheng just ignor it.

A phasor strip the time domain \omegat out, but the phase angle of incident E field is absolute a spatial domain and cannot be ignor. The solution from the two cannot be made equal to justify that.

I spent 2 days deriving the formulas and just can not make the two agree. I don't see how they can ignor the phase angle unless the incident E field at z=0 is always at maximum which is cosine(0)=1 like you suggested! But what is the justification that the forward traveling E field is ALWAYS maximum at z=0? I have modify my original equation drawing above, please take a look again.

 

[ravioli]

If you were given an oscilloscope, could you distinguish between the incident wave having a phase shift of 0 degrees, 10 degrees, 20 degrees, 30 degrees...?

 

[yungman]

If you were given an oscilloscope, could you distinguish between the incident wave having a phase shift of 0 degrees, 10 degrees, 20 degrees, 30 degrees...?

No! This is EM wave, not the voltage and current phasor in transmission. They are the same though, the same question apply on voltage phasor at z=0 at the load. A directional coupler can separate the incident and reflected. But getting to the z=0 is easy to talk, impossible to get to!

 

[yungman]

I have been looking up quite a few books today on both Plane Wave phasor and transmission line traveling wave phasor. All the books specified that the amplitude at z=0 is REAL. There is not phase angle. If the amplitude is real, then I agree with the book!

Can anyone give me a conclusive theory why the amplitude at z=0 is always real? The only book that claimed the value can be complex, that is Ulaby book.